#P4274. 第2题-最大能量路径
-
1000ms
Tried: 575
Accepted: 120
Difficulty: 5
所属公司 :
华为
时间 :2025年10月22日-AI方向
-
算法标签>动态规划
第2题-最大能量路径
思路
-
预处理能量: 先按上式计算整张图的能量矩阵 E,复杂度 O(H⋅W⋅K2)。
-
动态规划建模: 用 fi,j 表示走到位置 (i,j) 的最大能量和:
-
边界: fi,0=Ei,0,对所有 i∈[0,H−1]。
-
转移:
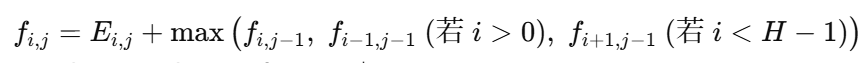
-
答案: 0≤i<Hmaxfi,W−1。 动规部分复杂度 O(H⋅W),总复杂度 O(H⋅W⋅K2),空间 O(H⋅W)(可滚动数组降到 O(H))。
-
-
实现细节:
- 第一行输入可能是用空格或反斜杠分隔,实际读取时可将反斜杠替换为空格再解析 H,W,K。
- 输出用固定小数位格式保留 1 位小数。
C++
#include <bits/stdc++.h>
using namespace std;
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
// 读取首行,兼容空格或反斜杠分隔
string first;
// 跳过可能的空行
do {
if (!getline(cin, first)) return 0;
} while (first.find_first_not_of(" \t\r\n") == string::npos);
for (char &c : first) if (c == '\\') c = ' ';
stringstream ss(first);
int H, W, K;
ss >> H >> W >> K;
// 读取图像矩阵
vector<vector<double>> I(H, vector<double>(W));
for (int i = 0; i < H; ++i) {
for (int j = 0; j < W; ++j) {
cin >> I[i][j];
}
}
// 读取策略(卷积核)矩阵
vector<vector<double>> P(K, vector<double>(K));
for (int i = 0; i < K; ++i) {
for (int j = 0; j < K; ++j) {
cin >> P[i][j];
}
}
// 计算能量矩阵 E,按0填充的卷积(相关)方式
vector<vector<double>> E(H, vector<double>(W, 0.0));
int pad = K / 2;
for (int i = 0; i < H; ++i) {
for (int j = 0; j < W; ++j) {
double s = 0.0;
// 遍历核
for (int a = 0; a < K; ++a) {
for (int b = 0; b < K; ++b) {
int ii = i + a - pad;
int jj = j + b - pad;
if (0 <= ii && ii < H && 0 <= jj && jj < W) {
s += P[a][b] * I[ii][jj];
}
}
}
E[i][j] = s;
}
}
// 动态规划:从第0列走到第W-1列,允许右、右上、右下
vector<vector<double>> dp(H, vector<double>(W, -1e300));
for (int i = 0; i < H; ++i) dp[i][0] = E[i][0];
for (int j = 1; j < W; ++j) {
for (int i = 0; i < H; ++i) {
double best = dp[i][j-1];
if (i > 0) best = max(best, dp[i-1][j-1]);
if (i + 1 < H) best = max(best, dp[i+1][j-1]);
dp[i][j] = best + E[i][j];
}
}
double ans = -1e300;
for (int i = 0; i < H; ++i) ans = max(ans, dp[i][W-1]);
cout.setf(std::ios::fixed);
cout << setprecision(1) << ans << "\n";
return 0;
}
import sys
def main():
data = sys.stdin.read().strip().split()
it = iter(data)
H = int(next(it)); W = int(next(it)); K1 = int(next(it)); K2 = int(next(it))
K = K1 # 题面给了两个K,这里取第一个;通常两者相等
# 读图像矩阵
I = [[float(next(it)) for _ in range(W)] for _ in range(H)]
# 读策略矩阵
P = [[float(next(it)) for _ in range(K)] for _ in range(K)]
# 计算能量图(零填充卷积)
r = K // 2
E = [[0.0]*W for _ in range(H)]
for i in range(H):
for j in range(W):
s = 0.0
for u in range(K):
ii = i + (u - r)
if 0 <= ii < H:
rowI = I[ii]
rowP = P[u]
for v in range(K):
jj = j + (v - r)
if 0 <= jj < W:
s += rowP[v] * rowI[jj]
E[i][j] = s
# 动态规划
NEG = -1e300
prev = [NEG]*H
for i in range(H):
prev[i] = E[i][0]
for j in range(1, W):
cur = [NEG]*H
for i in range(H):
best = prev[i]
if i-1 >= 0:
best = max(best, prev[i-1])
if i+1 < H:
best = max(best, prev[i+1])
cur[i] = E[i][j] + best
prev = cur
ans = max(prev)
print(f"{ans:.1f}")
if __name__ == "__main__":
main()
import java.io.*;
import java.util.*;
import java.util.Locale;
public class Main {
public static void main(String[] args) throws Exception {
Locale.setDefault(Locale.US); // 确保小数点为 '.'
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
List<Double> tokens = new ArrayList<>();
String line;
// 读取所有数字(支持以空格或换行分隔)
while ((line = br.readLine()) != null) {
line = line.trim();
if (line.isEmpty()) continue;
String[] parts = line.split("\\s+");
for (String p : parts) tokens.add(Double.parseDouble(p));
}
int idx = 0;
int H = tokens.get(idx++).intValue();
int W = tokens.get(idx++).intValue();
int K1 = tokens.get(idx++).intValue();
int K2 = tokens.get(idx++).intValue();
int K = K1; // 题面给了两个K
double[][] I = new double[H][W];
for (int i = 0; i < H; i++)
for (int j = 0; j < W; j++)
I[i][j] = tokens.get(idx++);
double[][] P = new double[K][K];
for (int i = 0; i < K; i++)
for (int j = 0; j < K; j++)
P[i][j] = tokens.get(idx++);
// 计算能量图(零填充卷积)
int r = K / 2;
double[][] E = new double[H][W];
for (int i = 0; i < H; i++) {
for (int j = 0; j < W; j++) {
double s = 0.0;
for (int u = 0; u < K; u++) {
int ii = i + (u - r);
if (0 <= ii && ii < H) {
for (int v = 0; v < K; v++) {
int jj = j + (v - r);
if (0 <= jj && jj < W) {
s += P[u][v] * I[ii][jj];
}
}
}
}
E[i][j] = s;
}
}
// 动态规划:只能右、右上、右下
double NEG = -1e300;
double[] prev = new double[H];
double[] cur = new double[H];
Arrays.fill(prev, NEG);
for (int i = 0; i < H; i++) prev[i] = E[i][0];
for (int j = 1; j < W; j++) {
Arrays.fill(cur, NEG);
for (int i = 0; i < H; i++) {
double best = prev[i];
if (i - 1 >= 0) best = Math.max(best, prev[i - 1]);
if (i + 1 < H) best = Math.max(best, prev[i + 1]);
cur[i] = E[i][j] + best;
}
double[] tmp = prev; prev = cur; cur = tmp;
}
double ans = NEG;
for (int i = 0; i < H; i++) ans = Math.max(ans, prev[i]);
System.out.printf("%.1f%n", ans);
}
}
题目内容
在自动驾驶系统中,车道线识别是核心功能之一。车道线通常具有连续性,从图像左侧到右侧逐渐展开。
为了识别出最可能的车道线路径,我们可以在图像中找到一条路径,使得路径上所有像素的信号值与策略矩阵的乘积之和最大。
现定义每个位置的能量值为策略矩阵与该位置周边信号值的乘积和。
给定一个 H×W 的图像以及一个 K×K 的策略矩阵,用于模拟不同方向的路径选择策略。
你需要从图像的第一列任意像素出发,走到最后一列任意像素,每一步只能向右、右上、右下移动一格。
在行进的过程中,需要实时的收集能量值,请找到一条路径,使得路径上的能量值之和最大。
输入描述
第一行输入 H W K K ,分表表示给定图像及策略矩阵的维度
接下来
H 行输入图像矩阵
K 行输入策略矩阵
输出描述
输出最大能量值
样例1
输入
1 1 1 1
5
1
输出
5.0
说明
有且仅有一条路径,最大能量值为 5∗1 为 5.0
样例2
输入
3 3 3 3
1 2 3
4 5 6
7 8 9
1 2 2
1 1 1
1 1 1
输出
119.0
说明
输入第一行是一个 3×3 的图像以及 3×3 的策略矩阵
每个位置的能量图:
[[12.21.16.]
[30.50.36.]
[33.50.34.]]
最大能量路径的值:119.0 最大能量路径:(2,0)−>(1,1)−>(1,2)
提示
1.策略矩阵为奇数,边缘处用零填充
2.输出保留一位小数
