思路：动态规划

将所有盒子按照长、宽、高的三个优先级进行从小到大的排序，那么后面的盒子一定不可能放在前面盒子的上面。所以我们排序之后，选择的顺序就已经是定死的从左往右选择了。那么可以使用动态规划进行求解。

定义$dp[i]$表示放上第$i$个盒子所能达到的最大高度，则有

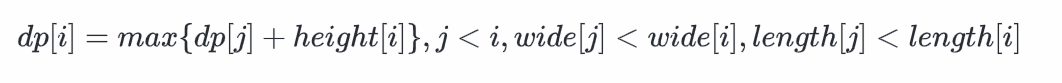
答案为$max{dp[i]},1\le i\le n$

解题思路

1. 排序：首先，将所有盒子按照长、宽、高三个维度进行从小到大的排序。由于后面的盒子在长、宽、高方面都大于前面的盒子，因此可以确保一个盒子不会被放在另一个盒子上面，从而简化了问题。

2. 动态规划：接下来，使用动态规划来解决问题。定义 dp[i] 表示以第 i 个盒子为顶部盒子时，所能达到的最大堆叠高度。我们需要考虑所有之前的盒子，如果一个盒子可以放在另一个盒子上面，就更新 dp[i] 的值。

3. 结果计算：最终，结果为所有 dp[i] 中的最大值，即为我们能够堆叠的最高高度。

代码

java

import java.util.Arrays;
import java.util.Scanner;

public class Main {
    static int n;
    static int[] dp;
    static Box[] box;

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        n = sc.nextInt();
        box = new Box[n + 1];
        dp = new int[n + 1];

        for (int i = 1; i <= n; i++) {
            box[i] = new Box(sc.nextInt(), sc.nextInt(), sc.nextInt());
        }

        Arrays.sort(box, 1, n + 1, (a, b) -> {
            if (a.l != b.l) {
                return a.l - b.l;
            }
            if (a.w != b.w) {
                return a.w - b.w;
            }
            return a.h - b.h;
        });

        int ans = 0;
        for (int i = 1; i <= n; i++) {
            dp[i] = box[i].h;
            for (int j = 1; j < i; j++) {
                if (box[i].h > box[j].h && box[i].l > box[j].l && box[i].w > box[j].w) {
                    dp[i] = Math.max(dp[i], dp[j] + box[i].h);
                }
            }
            ans = Math.max(ans, dp[i]);
        }
        System.out.println(ans);
        sc.close();
    }

    static class Box {
        int l, w, h;

        Box(int l, int w, int h) {
            this.l = l;
            this.w = w;
            this.h = h;
        }
    }
}

python

N=int(input())
box=[]
for _ in range(N):
    box.append(list(map(int,input().split())))

box.sort(key=lambda x:(x[0],x[1],x[2])) #升序排序

dp=[0]*N #对于每个盒子作为最底层，其可以获得的最大高度是多少

for i in range(N):
    dp[i]=box[i][2] #是其自己的高度
    for j in range(i):
        #遍历前面的盒子
        #如果比前一个盒子的长宽高都大，那就是自己的高度再加上j盒子的最大高度
        if box[i][0]>box[j][0] and box[i][1]>box[j][1] and box[i][2]>box[j][2]:
            dp[i]=max(dp[i],dp[j]+box[i][2])

print(max(dp))

C++

#include <bits/stdc++.h>
using namespace std;

const int maxn=1e3+10;
int dp[maxn];
int n;
struct node{
	int l, w, h;
}box[maxn];


int main(){
    cin>>n;
    for(int i=1;i<=n;++i){
    	cin>>box[i].l>>box[i].w>>box[i].h;
	}
    //长、宽、高的三个优先级进行从小到大的排序
    sort(box+1, box+n+1, [&](node a, node b){
		if(a.l!=b.l){
			return a.l<b.l;   
		}
		if(a.w!=b.w){
			return a.w<b.w;
		}
		return a.h<b.h;
	});
    int ans=0;
    //dp[i]表示放上第i个盒子所能达到的最大高度
    for(int i=1;i<=n;++i){
        dp[i]=box[i].h;
        for (int j = 1; j < i; j++) {
            if (box[i].h > box[j].h && box[i].l > box[j].l && box[i].w > box[j].w) {
                dp[i]=max(dp[i],dp[j]+box[i].h);
            }
        }
        ans = max(ans,dp[i]);
    }
    cout<<ans;
}

题目内容

圣诞节到了，小明的妈妈准备了很多圣诞礼盒，礼盒大小不同，小明在玩堆盒子的游戏，妈妈问小明，怎么堆盒子使得堆出的高度最高，每个礼盒的大小由长、宽、高表示，堆盒子的时候要求下面的盒子长、宽、高都必须大于上面的盒子，不包含等于。请你帮助小明一起堆出最高的一堆礼盒，高度为堆出的礼盒的所有高度的总和。

输入描述

输入的第一行是礼盒的个数$N$，

接下来输入$N$行，每行表示每个礼盒的长、宽、高。

礼盒的数量不超过$1000$个，每个盒子的长、宽、高取值范围为$1$~$10$。

输出描述

输出一行，输出能堆出盒子的最高高度

样例1

输入

4
1 1 1
2 3 4
3 6 7
4 5 6

输出

12

说明

选择$1、2、3$，$3$个盒子堆出的高度最高，$1+4+7=12$

样例2

输入

4
1 1 1
1 1 1
2 2 2
2 2 2

输出

3

说明

其中的一种选择方式为选择$1$和$3$两个盒子，堆出的高度最高为$1+2=3$