题目内容

果园里有各种果树，周末花花去果园里摘水果，果树的排列是一个 $n*n$ 的网格，每个网格中的数据表示果树可以采摘的水果数量。

为了保证采摘果树有序不被破坏，采摘果树只能从 $(0,0)$ 的位置出发，往某些特定的方向行走，直到走到 $(n-1,n-1)$ 位置再回头，出发时只能向下或者向右行走，回头时只能向上或向左行走回到原始位置 $(0,0)$，由于某些果树未成熟，通过路障进行保护，不让通过，每颗果树只能采摘一次，即去的路上采摘回来路上可以经过但不可以采摘。采摘水果只能进行一次来回。

网格中的数字有如下含义:

1、$0$ 表示没有果树可以采摘;

2、$-1$ 表示果树未成熟不能通过;

3、其他数值表示可以采摘的水果数量。

请你帮忙统计，花花在果园里最多可以采摘的水果数量。

输入描述

输入第一行是 $n$ 的大小，接下来输入 $n$ 行，表示 $n*n$ 的网格数量， $n$ 的取值范围为 $1$ ~ $100$ 。

注意每个网格来回经过只能算采摘一次。

输出描述

输出最多可以采摘的水果数量。

样例1

输入

3
0 2 0
1 -1 0
3 0 1

输出

7

说明

路径 $1$ ：从 $(0,0)$ 出发，向下、向下、向右、向右走到 $(2,2)$ ，这一行程中采摘 $5$ 个水果，然后向上、向上、向左、向左，返回起点，再采摘 $2$ 个水果，共采摘 $7$ 个水果。

如下图中红色的箭头是出发的线路，蓝色的箭头是回来的路线:

路径 $2$ ：从 $(0,0)$ 出发，向右、向右、向下、向下走到 $(2,2)$，这一行程中采摘 $3$ 个水果，然后向左、向左、向上、向上，返回起点，再采摘 $4$ 个水果，共采摘 $7$ 个水果。

两种路径均可

样例2

输入

4
2 0 1 -1
0 -1 3 1
2 0 1 0
4 -1 1 3

输出

14

说明

路径 $1$ ：从 $(0,0)$ 出发，向右、向右、向下、向右、向下、向下走到 $(3,3)$ ，这行程中采摘 $10$ 个水果，然后向左、向上、向左、向左、向上、向上，返回起点，再采摘 $4$ 个水果，共采摘 $14$ 个水果。

提示

在指定的行走规则下输出最多的可以采集的水果数量，只有一次来回。

题解

题面描述

果园里有一个 $n \times n$ 的网格，每个网格中的数字表示该位置的果树可以采摘的水果数量：

1. 0 表示没有果树可以采摘。
2. -1 表示果树未成熟，不能通过该位置。
3. 其他正整数表示可以采摘的水果数量。

花花需要从起点 $(0,0)$ 出发，按照以下规则进行采摘：

• 出发路径：只能向下或向右移动，直到到达终点 $(n-1,n-1)$。
• 回程路径：只能向上或向左移动，返回起点 $(0,0)$。

采摘水果时，每个果树只能采摘一次，即在出发和回程路径中，同一位置的水果只能被采摘一次。回程路径可以经过已采摘的果树，但不能再次采摘。

目标是找到一条满足上述条件的路径，使得花花可以采摘到的水果总数最大。

思路

这道题与经典的“樱桃采摘”问题类似。我们可以将整个来回采摘过程视为两个人从起点同时出发，最终同时到达终点的过程。为了避免重复采摘同一位置的水果，我们需要确保两条路径上相同位置的水果只被采摘一次。

具体来说，可以使用动态规划的方法来解决这个问题。设定一个三维的 DP 数组 dp[k][i][j]，其中：

• k 表示当前的步数。
• i 和 j 分别表示两个人在第 k 步时的行位置。
• 根据步数 k 和行位置 i，可以确定两个人的列位置分别为 k - i 和 k - j。

状态转移方程需要考虑两个人的移动方向，并且处理位置重叠时水果只被采摘一次的情况。同时，需要考虑障碍物（-1）的存在，如果某一步的位置为 -1，则该状态无效。

状态转移详细分析

为了计算 dp[k][i][j] 的值，我们需要考虑两条路径在第 k 步时可以从哪些位置转移过来。具体来说，两条路径在第 k-1 步时可以分别位于 (i-1, k-1 - (i-1)) 或 (i, k-1 - i)，以及 (j-1, k-1 - (j-1)) 或 (j, k-1 - j)。

因此，状态转移方程可以表示为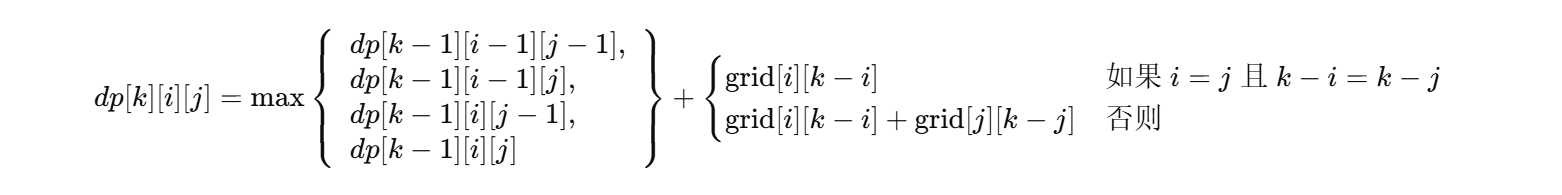： 具体解释如下：

1. 选择前一步的位置：

   • 第一条路径可以从上方 (i-1, k-1 - (i-1)) 或左方 (i, k-1 - i) 移动到 (i, k-i)。
   • 第二条路径可以从上方 (j-1, k-1 - (j-1)) 或左方 (j, k-1 - j) 移动到 (j, k-j)。

2. 计算当前步的水果数量：

   • 如果两条路径当前位置 (i, k-i) 和 (j, k-j) 是同一个位置，即 i == j 且 k-i == k-j，那么只采摘一次该位置的水果。
   • 否则，分别采摘两条路径当前位置的水果，即 grid[i][k-i] + grid[j][k-j]。

3. 考虑障碍物和无果树情况：

   • 如果当前位置 (i, k-i) 或 (j, k-j) 有障碍物 -1，则该状态不可达，dp[k][i][j] 设为 -1。

cpp

#include <bits/stdc++.h>
using namespace std;

int main(){
    int n;
    cin >> n;
    vector<vector<int>> grid(n, vector<int>(n));
    for(auto &row : grid) {
        for(auto &cell : row) cin >> cell;
    }

    // 初始化DP数组，dp[k][i][j] 表示第k步时，两人分别在(i, k-i)和(j, k-j)位置的最大水果数
    // 初始化所有状态为 -1，表示不可达
    // 步数 k 从 0 到 2*(n-1)
    vector<vector<vector<int>>> dp(2*n, vector<vector<int>>(n, vector<int>(n, -1)));

    // 初始状态
    if(grid[0][0] != -1){
        dp[0][0][0] = grid[0][0];
    }

    // 遍历所有步数 k
    for(int k = 1; k <= 2*(n-1); ++k){
        for(int i = 0; i < n; ++i){
            for(int j = 0; j < n; ++j){
                // 根据步数k和行坐标i、j计算列坐标y1和y2
                int y1 = k - i;
                int y2 = k - j;
                // 检查列坐标是否在范围内
                if(y1 < 0 || y1 >= n || y2 < 0 || y2 >= n){
                    continue;
                }
                // 获取两个人的位置
                int x1 = i, y_1 = y1;
                int x2 = j, y_2 = y2;
                // 如果当前位置有障碍，跳过
                if(grid[x1][y_1] == -1 || grid[x2][y_2] == -1){
                    continue;
                }
                // 计算前一步的最大值
                int res = -1;
                // 两个人的前一步可以来自上方或左方，共四种组合
                for(int pi = i-1; pi <= i; pi++){
                    for(int pj = j-1; pj <= j; pj++){
                        if(pi < 0 || pj < 0){
                            continue;
                        }
                        if(dp[k-1][pi][pj] == -1){
                            continue;
                        }
                        res = max(res, dp[k-1][pi][pj]);
                    }
                }
                if(res == -1){
                    continue;
                }
                // 计算当前步采摘的水果数
                if(x1 == x2 && y_1 == y2){
                    // 如果两人在同一个位置，只采摘一次
                    res += grid[x1][y_1];
                }
                else{
                    // 不同位置，分别采摘
                    res += grid[x1][y_1] + grid[x2][y_2];
                }
                // 更新dp[k][i][j]的值
                dp[k][i][j] = max(dp[k][i][j], res);
            }
        }
    }

    // 获取最终结果
    int result = dp[2*(n-1)][n-1][n-1];
    // 无需再减去终点的水果，因为在DP过程中已正确处理
    cout << (result < 0 ? 0 : result);
}

python

import sys

def main():
    n = int(sys.stdin.readline())
    grid = []
    for _ in range(n):
        grid.append(list(map(int, sys.stdin.readline().split())))

    # 初始化DP数组，dp[k][i][j] 表示第k步时，两人分别在(i, k-i)和(j, k-j)位置的最大水果数
    dp = [[[-1 for _ in range(n)] for _ in range(n)] for _ in range(2*n)]

    # 初始状态
    if grid[0][0] != -1:
        dp[0][0][0] = grid[0][0]

    # 遍历所有步数 k
    for k in range(1, 2*(n-1)+1):
        for i in range(n):
            for j in range(n):
                y1 = k - i
                y2 = k - j
                # 检查列坐标是否在范围内
                if y1 < 0 or y1 >= n or y2 < 0 or y2 >= n:
                    continue
                x1, y_1 = i, y1
                x2, y_2 = j, y2
                # 如果当前位置有障碍，跳过
                if grid[x1][y_1] == -1 or grid[x2][y_2] == -1:
                    continue
                # 计算前一步的最大值
                res = -1
                for pi in [i-1, i]:
                    for pj in [j-1, j]:
                        if pi < 0 or pj < 0:
                            continue
                        if dp[k-1][pi][pj] == -1:
                            continue
                        res = max(res, dp[k-1][pi][pj])
                if res == -1:
                    continue
                # 计算当前步采摘的水果数
                if x1 == x2 and y_1 == y2:
                    # 如果两人在同一个位置，只采摘一次
                    res += grid[x1][y_1]
                else:
                    # 不同位置，分别采摘
                    res += grid[x1][y_1] + grid[x2][y_2]
                # 更新dp[k][i][j]的值
                dp[k][i][j] = max(dp[k][i][j], res)

    # 获取最终结果
    result = dp[2*(n-1)][n-1][n-1]
    # 无需再减去终点的水果，因为在DP过程中已正确处理
    print(max(result, 0))

if __name__ == "__main__":
    main()

java

import java.util.*;

public class Main{
    public static void main(String[] args){
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        int[][] grid = new int[n][n];
        for(int i=0;i<n;i++) {
            for(int j=0;j<n;j++) {
                grid[i][j] = sc.nextInt();
            }
        }

        // 初始化DP数组，dp[k][i][j] 表示第k步时，两人分别在(i, k-i)和(j, k-j)位置的最大水果数
        int[][][] dp = new int[2*n][n][n];
        for(int k=0; k<2*n; k++){
            for(int i=0; i<n; i++){
                Arrays.fill(dp[k][i], -1);
            }
        }

        // 初始状态
        if(grid[0][0] != -1){
            dp[0][0][0] = grid[0][0];
        }

        // 遍历所有步数 k
        for(int k=1; k<=2*(n-1); k++){
            for(int i=0; i<n; i++){
                for(int j=0; j<n; j++){
                    int y1 = k - i;
                    int y2 = k - j;
                    // 检查列坐标是否在范围内
                    if(y1 < 0 || y1 >= n || y2 < 0 || y2 >= n){
                        continue;
                    }
                    int x1 = i, y_1 = y1;
                    int x2 = j, y_2 = y2;
                    // 如果当前位置有障碍，跳过
                    if(grid[x1][y_1] == -1 || grid[x2][y_2] == -1){
                        continue;
                    }
                    // 计算前一步的最大值
                    int res = -1;
                    // 两个人的前一步可以来自上方或左方，共四种组合
                    for(int pi = i-1; pi <= i; pi++){
                        for(int pj = j-1; pj <= j; pj++){
                            if(pi < 0 || pj < 0){
                                continue;
                            }
                            if(dp[k-1][pi][pj] == -1){
                                continue;
                            }
                            res = Math.max(res, dp[k-1][pi][pj]);
                        }
                    }
                    if(res == -1){
                        continue;
                    }
                    // 计算当前步采摘的水果数
                    if(x1 == x2 && y_1 == y2){
                        // 如果两人在同一个位置，只采摘一次
                        res += grid[x1][y_1];
                    }
                    else{
                        // 不同位置，分别采摘
                        res += grid[x1][y_1] + grid[x2][y_2];
                    }
                    // 更新dp[k][i][j]的值
                    dp[k][i][j] = Math.max(dp[k][i][j], res);
                }
            }
        }

        // 获取最终结果
        int result = dp[2*(n-1)][n-1][n-1];
        // 无需再减去终点的水果，因为在DP过程中已正确处理
        System.out.println(result < 0 ? 0 : result);
    }
}