模型与目标

• 线性部分：$O=XW+b$，其中 $X\in\mathbb{R}^{N\times n}$、$W\in\mathbb{R}^{n\times k}$、$b\in\mathbb{R}^{1\times k}$。

• 概率：$P$=$\mathrm{softmax}(O)$，对每行做 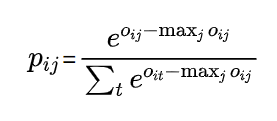（减去按行最大值做数值稳定）。

• 损失（带 $L_2$ 正则）：

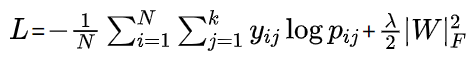
• 梯度：

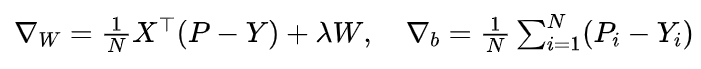
• 预测：对每个样本取 $\arg\max_j p_{ij}$ 得到分类 $0\sim k-1$。

C++

#include <bits/stdc++.h>
using namespace std;

// 说明：实现一个多分类 softmax 回归，使用全批量梯度下降与L2正则。
// 输入：n, k, 每类样本数（k个），m；随后 N 行训练样本、m 行待预测样本
// 输出：m 行，每行一个预测类别编号

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    int n, k;
    if (!(cin >> n >> k)) return 0;

    vector<int> cnt(k);
    long long N = 0;
    for (int i = 0; i < k; ++i) { cin >> cnt[i]; N += cnt[i]; }

    int m; cin >> m;

    // 读取训练数据
    vector<vector<double>> X_train(N, vector<double>(n, 0.0));
    for (long long i = 0; i < N; ++i) {
        for (int j = 0; j < n; ++j) cin >> X_train[i][j];
    }

    // 生成标签（按类别顺序）
    vector<int> y_train;
    y_train.reserve(N);
    for (int c = 0; c < k; ++c) {
        for (int t = 0; t < cnt[c]; ++t) y_train.push_back(c);
    }

    // 读取待预测数据
    vector<vector<double>> X_test(m, vector<double>(n, 0.0));
    for (int i = 0; i < m; ++i) {
        for (int j = 0; j < n; ++j) cin >> X_test[i][j];
    }

    // 特征标准化：计算均值和标准差（仅训练集）
    const double eps = 1e-8;
    vector<double> mu(n, 0.0), sigma(n, 0.0);
    for (int j = 0; j < n; ++j) {
        double s = 0.0;
        for (long long i = 0; i < N; ++i) s += X_train[i][j];
        mu[j] = (N ? s / N : 0.0);
    }
    for (int j = 0; j < n; ++j) {
        double ss = 0.0;
        for (long long i = 0; i < N; ++i) {
            double d = X_train[i][j] - mu[j];
            ss += d * d;
        }
        sigma[j] = sqrt((N ? ss / max(1LL, N - 1) : 0.0));
        if (sigma[j] < eps) sigma[j] = 1.0; // 方差过小则置1
    }
    auto standardize = [&](vector<vector<double>>& X) {
        for (auto &row : X) {
            for (int j = 0; j < n; ++j) row[j] = (row[j] - mu[j]) / (sigma[j] + eps);
        }
    };
    standardize(X_train);
    standardize(X_test);

    // 参数：W (n x k), b (k)
    vector<vector<double>> W(n, vector<double>(k, 0.0));
    vector<double> b(k, 0.0);

    // 训练超参
    int epochs = 600;        // 训练轮数
    double lr = 0.1;         // 学习率
    double reg = 1e-4;       // L2 正则

    // 训练
    vector<double> logits(k), probs(k);
    for (int epoch = 0; epoch < epochs; ++epoch) {
        // 梯度清零
        vector<vector<double>> dW(n, vector<double>(k, 0.0));
        vector<double> db(k, 0.0);

        // 全批量：逐样本累积梯度
        for (long long i = 0; i < N; ++i) {
            // 计算 logits = X_i * W + b
            for (int j = 0; j < k; ++j) {
                double s = b[j];
                for (int f = 0; f < n; ++f) s += X_train[i][f] * W[f][j];
                logits[j] = s;
            }
            // softmax（数值稳定：减最大值）
            double mx = *max_element(logits.begin(), logits.end());
            double sumExp = 0.0;
            for (int j = 0; j < k; ++j) { probs[j] = exp(logits[j] - mx); sumExp += probs[j]; }
            for (int j = 0; j < k; ++j) probs[j] /= (sumExp + eps);

            // 残差 = p - y_onehot
            int y = y_train[i];
            for (int j = 0; j < k; ++j) {
                double diff = probs[j] - (j == y ? 1.0 : 0.0);
                // 累积 dW 与 db
                for (int f = 0; f < n; ++f) dW[f][j] += X_train[i][f] * diff;
                db[j] += diff;
            }
        }
        // 平均并加正则
        double invN = (N ? 1.0 / (double)N : 1.0);
        for (int f = 0; f < n; ++f) {
            for (int j = 0; j < k; ++j) {
                dW[f][j] = dW[f][j] * invN + reg * W[f][j];
            }
        }
        for (int j = 0; j < k; ++j) db[j] *= invN;

        // 参数更新
        for (int f = 0; f < n; ++f)
            for (int j = 0; j < k; ++j)
                W[f][j] -= lr * dW[f][j];
        for (int j = 0; j < k; ++j) b[j] -= lr * db[j];

        // 可选：学习率轻微衰减（稳定训练）
        if ((epoch + 1) % 150 == 0) lr *= 0.9;
    }

    // 预测
    for (int i = 0; i < m; ++i) {
        for (int j = 0; j < k; ++j) {
            double s = b[j];
            for (int f = 0; f < n; ++f) s += X_test[i][f] * W[f][j];
            logits[j] = s;
        }
        int argmax = 0;
        for (int j = 1; j < k; ++j) if (logits[j] > logits[argmax]) argmax = j;
        cout << argmax << "\n";
    }
    return 0;
}

Python

# 说明：多分类 softmax 回归，使用全批量梯度下降与L2正则
# 输入输出同题面描述

import sys
import math

def read_ints():
    return list(map(float, sys.stdin.readline().strip().split()))

# 为了稳妥处理空白行，使用迭代读取
tokens = []
for line in sys.stdin:
    parts = line.strip().split()
    if parts:
        tokens.extend(parts)

it = iter(tokens)
def next_int():
    return int(next(it))
def next_float():
    return float(next(it))

n = next_int()
k = next_int()
cnt = [next_int() for _ in range(k)]
N = sum(cnt)
m = next_int()

# 读取训练与预测
X_train = [[next_float() for _ in range(n)] for _ in range(N)]
y_train = []
for c in range(k):
    for _ in range(cnt[c]):
        y_train.append(c)
X_test = [[next_float() for _ in range(n)] for _ in range(m)]

# 标准化
eps = 1e-8
mu = [0.0]*n
sigma = [0.0]*n

for j in range(n):
    s = sum(X_train[i][j] for i in range(N)) if N > 0 else 0.0
    mu[j] = s / N if N > 0 else 0.0
for j in range(n):
    ss = 0.0
    for i in range(N):
        d = X_train[i][j] - mu[j]
        ss += d*d
    sigma[j] = math.sqrt((ss / max(1, N-1))) if N > 1 else 1.0
    if sigma[j] < eps: sigma[j] = 1.0

def standardize(X):
    for i in range(len(X)):
        row = X[i]
        for j in range(n):
            row[j] = (row[j] - mu[j]) / (sigma[j] + eps)

standardize(X_train)
standardize(X_test)

# 参数
W = [[0.0]*k for _ in range(n)]
b = [0.0]*k

# 超参
epochs = 600
lr = 0.1
reg = 1e-4

# 训练
for epoch in range(epochs):
    dW = [[0.0]*k for _ in range(n)]
    db = [0.0]*k

    for i in range(N):
        # logits
        logits = [b[j] + sum(X_train[i][f]*W[f][j] for f in range(n)) for j in range(k)]
        mx = max(logits)
        exps = [math.exp(v - mx) for v in logits]
        s = sum(exps) + eps
        probs = [v/s for v in exps]

        y = y_train[i]
        for j in range(k):
            diff = probs[j] - (1.0 if j == y else 0.0)
            for f in range(n):
                dW[f][j] += X_train[i][f] * diff
            db[j] += diff

    invN = (1.0 / N) if N > 0 else 1.0
    for f in range(n):
        for j in range(k):
            dW[f][j] = dW[f][j] * invN + reg * W[f][j]
    for j in range(k):
        db[j] *= invN

    for f in range(n):
        for j in range(k):
            W[f][j] -= lr * dW[f][j]
    for j in range(k):
        b[j] -= lr * db[j]

    if (epoch + 1) % 150 == 0:
        lr *= 0.9  # 轻微衰减

# 预测
out_lines = []
for i in range(m):
    logits = [b[j] + sum(X_test[i][f]*W[f][j] for f in range(n)) for j in range(k)]
    argmax = max(range(k), key=lambda j: logits[j])
    out_lines.append(str(argmax))

print("\n".join(out_lines))

Java

import java.io.*;
import java.util.*;

// 说明：多分类 softmax 回归，使用全批量梯度下降与L2正则
public class Main {
    static class FastScanner {
        private final InputStream in;
        private final byte[] buffer = new byte[1 << 16];
        private int ptr = 0, len = 0;
        FastScanner(InputStream is) { in = is; }
        private int read() throws IOException {
            if (ptr >= len) {
                len = in.read(buffer);
                ptr = 0;
                if (len <= 0) return -1;
            }
            return buffer[ptr++];
        }
        String next() throws IOException {
            StringBuilder sb = new StringBuilder();
            int c;
            while ((c = read()) <= ' ' && c != -1) ;
            if (c == -1) return null;
            do { sb.append((char)c); c = read(); } while (c > ' ');
            return sb.toString();
        }
        int nextInt() throws IOException { return Integer.parseInt(next()); }
        double nextDouble() throws IOException { return Double.parseDouble(next()); }
    }

    public static void main(String[] args) throws Exception {
        FastScanner fs = new FastScanner(System.in);
        String token = fs.next();
        if (token == null) return;
        int n = Integer.parseInt(token);
        int k = Integer.parseInt(fs.next());

        int[] cnt = new int[k];
        long N = 0;
        for (int i = 0; i < k; i++) { cnt[i] = Integer.parseInt(fs.next()); N += cnt[i]; }
        int m = Integer.parseInt(fs.next());

        double[][] Xtrain = new double[(int)N][n];
        for (int i = 0; i < N; i++) {
            for (int j = 0; j < n; j++) Xtrain[i][j] = fs.nextDouble();
        }
        int[] y = new int[(int)N];
        int idx = 0;
        for (int c = 0; c < k; c++) {
            for (int t = 0; t < cnt[c]; t++) y[idx++] = c;
        }
        double[][] Xtest = new double[m][n];
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) Xtest[i][j] = fs.nextDouble();
        }

        // 标准化
        double eps = 1e-8;
        double[] mu = new double[n];
        double[] sigma = new double[n];
        Arrays.fill(mu, 0.0);
        Arrays.fill(sigma, 0.0);

        for (int j = 0; j < n; j++) {
            double s = 0.0;
            for (int i = 0; i < N; i++) s += Xtrain[i][j];
            mu[j] = (N > 0) ? s / N : 0.0;
        }
        for (int j = 0; j < n; j++) {
            double ss = 0.0;
            for (int i = 0; i < N; i++) {
                double d = Xtrain[i][j] - mu[j];
                ss += d * d;
            }
            sigma[j] = (N > 1) ? Math.sqrt(ss / Math.max(1, (int)N - 1)) : 1.0;
            if (sigma[j] < eps) sigma[j] = 1.0;
        }
        standardizeInPlace(Xtrain, mu, sigma, eps);
        standardizeInPlace(Xtest, mu, sigma, eps);

        // 参数
        double[][] W = new double[n][k];
        double[] b = new double[k];

        // 超参
        int epochs = 600;
        double lr = 0.1;
        double reg = 1e-4;

        // 训练
        double[][] dW = new double[n][k];
        double[] db = new double[k];
        double[] logits = new double[k];
        double[] probs = new double[k];

        for (int epoch = 0; epoch < epochs; epoch++) {
            // 梯度清零
            for (int f = 0; f < n; f++) Arrays.fill(dW[f], 0.0);
            Arrays.fill(db, 0.0);

            for (int i = 0; i < N; i++) {
                // logits
                for (int j = 0; j < k; j++) {
                    double s = b[j];
                    for (int f = 0; f < n; f++) s += Xtrain[i][f] * W[f][j];
                    logits[j] = s;
                }
                // softmax（数值稳定）
                double mx = logits[0];
                for (int j = 1; j < k; j++) if (logits[j] > mx) mx = logits[j];
                double sumExp = 0.0;
                for (int j = 0; j < k; j++) {
                    probs[j] = Math.exp(logits[j] - mx);
                    sumExp += probs[j];
                }
                sumExp += eps;
                for (int j = 0; j < k; j++) probs[j] /= sumExp;

                int yy = y[i];
                for (int j = 0; j < k; j++) {
                    double diff = probs[j] - (j == yy ? 1.0 : 0.0);
                    for (int f = 0; f < n; f++) dW[f][j] += Xtrain[i][f] * diff;
                    db[j] += diff;
                }
            }

            double invN = (N > 0) ? (1.0 / N) : 1.0;
            for (int f = 0; f < n; f++) {
                for (int j = 0; j < k; j++) {
                    dW[f][j] = dW[f][j] * invN + reg * W[f][j];
                }
            }
            for (int j = 0; j < k; j++) db[j] *= invN;

            for (int f = 0; f < n; f++)
                for (int j = 0; j < k; j++)
                    W[f][j] -= lr * dW[f][j];
            for (int j = 0; j < k; j++) b[j] -= lr * db[j];

            if ((epoch + 1) % 150 == 0) lr *= 0.9; // 轻微衰减
        }

        // 预测
        StringBuilder sb = new StringBuilder();
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < k; j++) {
                double s = b[j];
                for (int f = 0; f < n; f++) s += Xtest[i][f] * W[f][j];
                logits[j] = s;
            }
            int argmax = 0;
            for (int j = 1; j < k; j++) if (logits[j] > logits[argmax]) argmax = j;
            sb.append(argmax).append('\n');
        }
        System.out.print(sb.toString());
    }

    static void standardizeInPlace(double[][] X, double[] mu, double[] sigma, double eps) {
        int rows = X.length, n = mu.length;
        for (int i = 0; i < rows; i++) {
            for (int j = 0; j < n; j++) {
                X[i][j] = (X[i][j] - mu[j]) / (sigma[j] + eps);
            }
        }
    }
}

题目内容

数据中心的机房需要散热，一般通过水冷系统调控机房的温度。出于节能的目的，需要收集数据中心最近一段时间的业务负裁，同时结合历史信息，外界气温、湿度等因素调高或调低冷机的出水温度。

逻辑回归是比轻量的模型，其输出 $0$ 或 $1$ 可以分别表示调低或调高温度。

在实际使用场景中，仅判断调低或调高不能满足业务要求，需要细化到调低 $1$ 度、调高 $0.5$度、维持不变、调高 $0.5$ 度、调高 $1$ 度等不同的"档位"。

因此，可以对逻辑回归进行改造，将其输出更改为 $softmax$ 可满足要求。

请根据提供的观测数据，训练改造后的模型，并根据给定样本数据预测调节的档位。

优化后的模型：$O=XW+b，P=softmax(O)$。

$X∈R(m,n)$ 表示 $m$ 条样本，每个样本有 $n$ 个特征；

$W∈R(n,k)$ 为权重；$k$ 是档位数(即 $k$ 个分类)；

$b∈R(1,k)$ 为偏置。$W$ 和 $b$ 通过训练得到。

$P∈R(m,k)$ 表示预测的概率，取概率最大的作为输出档位。

输入描述

1.第一行是数据 $schema$，分别表示特征数 $n$ ，分类数 $k$ ，第 $0$ 类样本数(即档位 $0$ )，第 $1$ 类样本数$，…，$第 $k-1$ 类样本数，待预测样本数 $m$ ；数据均为 $int$ 类型

2.后续的多行是 $k$ 个分类的训练样本(按照分类 $0$ 的多条样本、分类 $1$ 的多条样本 $、…$ 依次排列，一行一个样本)和 $m$ 条待预测样本(一行个样本)；数据均为 $float$ 类型

输出描述

每个待预测样本所所属的分类，一行输出一个样本的预测结果

样例1

输入

2 3 2 3 2 3
9 95
33 53
53 55
69 21
68 31
70 85
80 83
25 70
45 30
79 86

输出

0
1
2

说明

1.第一行数据 $2$ $3$ $2$ $3$ $2$ $3$ ，表示每条样本 $2$ 个特征，共有 $3$ 个分类；分类 $0$ 样本 $2$ 条，分类 $1$ 样本 $3$ 条，分类 $2$ 样本 $2$ 条；测试用例 $3$ 条

2.第 $2$~$3$ 行为分类 $0$ 样本(标签为 $0$ )，$4$~$6$ 行为分类 $1$ 样本(标签 $1$ )，$7$~$8$ 行为分类 $2$ 样本(标签为 $2$ )

3.最后 $3$ 行是待预测样本

输出：$3$ 个待预测样本的预测结果为分类 $0$ 、分类 $1$ 、分类 $2$

样例2

输入

3 3 4 3 4 5
9 95 7
33 53 13
45 43 6
40 50 11
53 55 36
69 21 55
68 31 43
70 85 23
80 83 46
70 73 55
76 78 53
25 70 6
20 69 16
45 30 50
79 86 51
70 76 36

输出

0
0
1
2
2

说明

1、第一行数据 $3$ $3$ $4$ $3$ $4$ $5$ ，表示每条样本 $3$ 个特征，共有 $3$ 个分类；分类 $0$ 样本 $4$ 条，分类 $1$ 样本 $3$ 条，分类 $2$ 样本 $4$ 条；测试用例 $5$ 条

2.第 $2$~$5$ 行为分类 $0$ 样本(标签为 $0$)，$6$~$8$ 行为分类 $1$ 样本(标签 $1$ )，$9$~$12$ 行为分类 $2$ 样本(标签为 $2$ )

3.最后 $5$ 行是待预测样本

输出：

$5$ 个待预测样本的预测结果为分类 $0$ (即档位 $0$ )、分类 $0$ 、分类 $1$ 、分类 $2$ 、分类 $2$

提示

1.使用交叉熵损失函数，标签值需转为 $one-hot$ 编码；梯度求解函数如下方公式所示，$Y$ 为真实标签(即 $one-hot$ 编码)；$P$ 为预测的概率(即 $softmax$ 的输出)

2.采用批梯度下降优化参数；选择比较好的学习率(根据经验，为了加快收敛速度，初始学习率可设置较大的数值，例如 $5$ )；适当增加迭代次数有助于获得更精确的结果；

3.原始数据值域一般在 $100$ 以内，为避免计算 $softmax$ 越界，需要对数据集执行归一化操作。

交叉熵函数

$-\frac{1}{m} \sum_{i=1}^{m} \sum_{j=1}^{k} Y_{i, j} \log \left(P_{i, j}\right)$

损失函数对 $W$ 的梯度

$\frac{1}{m} X^{T}(P-Y)$

损失函数对 $b$ 的梯度

$\frac{1}{m} \sum_{i=1}^{m}\left(P_{i,:}-Y_{i,:}\right)$