思路

• 设从 $i$ 向右行驶的每一步电量改变量为 $\Delta_k=a_k-a_{k+1}$。从 $i$ 出发到 $j$ 的前缀和为 $\sum_{t=i}^{j-1}(a_t-a_{t+1})=a_i-a_j$（望文生义的“望远镜求和”）。

• 为使过程中电量不为负，初始电量需至少抵消最小前缀和：

  • 向右所需：$\max\bigl(0,\ \max_{j\in[i,n]} a_j - a_i\bigr)$
  • 向左所需：$\max\bigl(0,\ \max_{j\in[1,i]} a_j - a_i\bigr)$

• 题目要求到达任意一端的最小初始电量，即二者取最小：

  

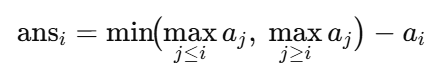
• 预处理前缀最大值 $\text{prefMax}[i]=\max_{1\le j\le i} a_j$ 与后缀最大值 $\text{sufMax}[i]=\max_{i\le j\le n} a_j$，则

  $\text{ans}_i$=$\min$($\text{prefMax}[i]$,$\text{sufMax}[i]$)-$a_i$

• 复杂度：时间 $O(n)$，空间 $O(n)$。

C++

#include <bits/stdc++.h>
using namespace std;

int main() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr);
	int n;
	if (!(cin >> n)) return 0;
	vector<long long> a(n + 1);
	for (int i = 1; i <= n; ++i) cin >> a[i];

	// 前缀最大值和后缀最大值
	vector<long long> pref(n + 1), suf(n + 2);
	for (int i = 1; i <= n; ++i) {
		pref[i] = (i == 1 ? a[i] : max(pref[i - 1], a[i]));
	}
	for (int i = n; i >= 1; --i) {
		suf[i] = (i == n ? a[i] : max(suf[i + 1], a[i]));
	}

	// 计算答案：min(pref[i], suf[i]) - a[i]
	for (int i = 1; i <= n; ++i) {
		long long need = min(pref[i], suf[i]) - a[i];
		if (i > 1) cout << ' ';
		cout << need;
	}
	cout << '\n';
	return 0;
}

Python

import sys

def solve():
    data = sys.stdin.read().strip().split()
    if not data:
        return
    it = iter(data)
    n = int(next(it))
    a = [0] + [int(next(it)) for _ in range(n)]

    # 前缀最大值
    pref = [0] * (n + 1)
    for i in range(1, n + 1):
        pref[i] = a[i] if i == 1 else max(pref[i - 1], a[i])

    # 后缀最大值
    suf = [0] * (n + 2)
    for i in range(n, 0, -1):
        suf[i] = a[i] if i == n else max(suf[i + 1], a[i])

    # 计算答案
    ans = [str(min(pref[i], suf[i]) - a[i]) for i in range(1, n + 1)]
    print(" ".join(ans))

if __name__ == "__main__":
    solve()

Java

import java.io.*;
import java.util.*;

public class Main {
	public static void main(String[] args) throws Exception {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		String s = br.readLine();
		if (s == null || s.isEmpty()) return;
		int n = Integer.parseInt(s.trim());
		String[] parts = br.readLine().trim().split("\\s+");
		long[] a = new long[n + 1];
		for (int i = 1; i <= n; i++) a[i] = Long.parseLong(parts[i - 1]);

		// 前缀最大值
		long[] pref = new long[n + 1];
		for (int i = 1; i <= n; i++) {
			pref[i] = (i == 1) ? a[i] : Math.max(pref[i - 1], a[i]);
		}
		// 后缀最大值
		long[] suf = new long[n + 2];
		for (int i = n; i >= 1; i--) {
			suf[i] = (i == n) ? a[i] : Math.max(suf[i + 1], a[i]);
		}

		// 计算答案
		StringBuilder sb = new StringBuilder();
		for (int i = 1; i <= n; i++) {
			long need = Math.min(pref[i], suf[i]) - a[i];
			if (i > 1) sb.append(' ');
			sb.append(need);
		}
		System.out.println(sb.toString());
	}
}

题目内容

给定一个长度为 $n$ 的山脉序列 $a=${ $a_1,a_2,…,a_n$ }，其中第 $i$ 个元素 $a_i$ 表示第 $i$ 座山的高度。电动汽车可以从任意位置 $i$ 出发，选择一直向左或一直向右行驶，直到山脉的端点。

行驶规则如下，当从一座高度为 $h$ 的山行驶到相邻一座高度为 $h_1$ 的山时：

• 若 $h_1 ≥ h_2$ (下坡)，电量增加 $h_1 -h_2$ ;

• 若 $h_1 < h_2$ (上坡)，电量消耗 $h_2 -h_1$ 。

对于每一个可能的出发点 $i(1 ≤i≤n)$ ，你需要分别计算，若选择从 $i$ 出发并一直向左行驶，或从 $i$ 出发并一直向右行驶，两种情况下为了保证行驶过程中电量始终不为负，所需的最小初始电量。

输入描述

第一行输入一个整数 $n(1 ≤n≤ 10^5)$ ，表示山脉序列的长度。

第二行输入 $n$ 个整数 $a_1,a_2,···,a_n(0≦a_i≦10^9)$ ，表示山脉的高度。

输出描述

输出一行 $n$ 个整数，用空格隔开。第 $i$ 个整数表示从位置 $i$ 出发，到达任意一端所需的最小初始电量。

样例1

输入

5
3 1 2 2 3

输出

0 2 1 1 0