思路

1.观察到每个数最多修改一次，那么显然最优的修改方案一定是前$i$小都乘以2，前$k-i$大都除以2。

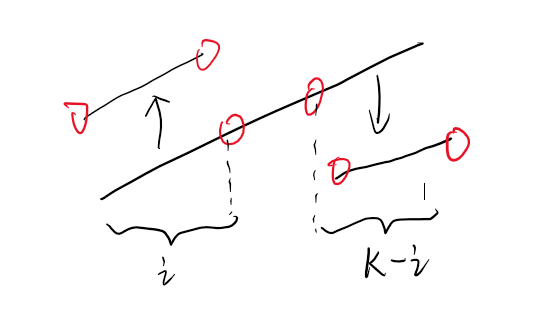
2.那么排序,枚举$i$然后模拟这个过程，去求最大值最小值，复杂度达到$O(n^2)$ 。但好在我们只关心极差，即最大值和最小值，所以不需要去模拟操作每一个数。而是考虑一次操作后结果会分成三段,分别去求这三段的最值就好了。如下图所示,我们只需要从这六个红圈中取极值即可。

代码

c++

#include <bits/stdc++.h>
using namespace std;

int in() {
	int x;
	cin >> x;
	return x;
}
int main()
{
	int n = in(), k = in();
    int a[n];
    for (int i = 0; i < n; i++) {
        a[i] = in();
    }
    sort(a, a+n);			//排序
    int ans = (int)1e9;
    for (int i = 0; i <= k; i++) {		//枚举修改前i小
        //三者不一定都存在，所以最小值初始化为一个较大的值，最大值初始化为一个小的值，再用三者更新
        int mi = (int)1e9, mx = 0;		
        if(i > 0) {		// 第一段的端点
            mi = min(mi, a[0]*2);
            mx = max(mx, a[i-1]*2);
        }
        if(k-i > 0) {	// 第三段的端点
            mi = min(mi, a[n-(k-i)]/2);
            mx = max(mx, a[n-1]/2);
        }
        if(n != k) {	// 第二段的端点
            mi = min(mi, a[i]);
            mx = max(mx, a[n-(k-i)-1]);
        }
        ans = min(ans, mx - mi);		//更新极差最小值
    }
    cout << ans << endl;
}

java

import java.util.*;
class Main {
    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        int n = in.nextInt(), k = in.nextInt();
        int[] a = new int[n];
        for (int i = 0; i < n; i++) {
            a[i] = in.nextInt();
        }
        Arrays.sort(a);			//排序
        int ans = (int)1e9;
        for (int i = 0; i <= k; i++) {		
            int mi = (int)1e9, mx = 0;		
            if(i > 0) {		
                mi = Math.min(mi, a[0]*2);
                mx = Math.max(mx, a[i-1]*2);
            }
            if(k-i > 0) {	
                mi = Math.min(mi, a[n-(k-i)]/2);
                mx = Math.max(mx, a[n-1]/2);
            }
            if(n != k) {	
                mi = Math.min(mi, a[i]);
                mx = Math.max(mx, a[n-(k-i)-1]);
            }
            ans = Math.min(ans, mx - mi);		
        }
        System.out.println(ans);
    }
}

题目内容

在一个遥远的王国里，有一座高耸入云的宝塔，据说里面藏有神秘的宝藏。但是，进入宝塔的道路异常困难，需要经过各种险阻，其中一个重要的关卡是“平衡之门”。

平衡之门是一条走廊，两边是无数个数码显示屏幕，每个屏幕上都显示着一个整数。在走廊中央有一个控制台，上面有两个按钮，一个是“乘2”按钮，一个是“除以2”按钮。每次按下其中一个按钮，控制台上的数字就会相应地变化。走廊中的每个数字最多只能被操作一次。

王国的宝藏猎人们想要通过平衡之门，以最小的代价进入宝塔。他们发现，只需要选择恰好 $k$ 个数字，使得每个数字经过不超过一次的操作后，可以得到所有的数字，就可以顺利通过平衡之门。现在他们需要你的帮助，计算出最小的极差，即经过操作后最大值和最小值之差的最小值。

输入描述

第一行输入两个正整数 $n$ 和 $k$ ，代表数组长度以及选择的元素数量。

第二行输入$n$个元素，代表给定的数组。

$1 \leq k \leq n \leq 10^5$

$1 \leq a_i \leq 10^9$

输出描述

$k$ 次操作后，数组极差的最小值。

样例$1$

输入输出示例仅供调试，后台判题数据一般不包含示例

输入

4 2
1 4 3 5

输出

2

样例$2$

输入

6 1
9 4 3 4 2 5

输出

3