思路

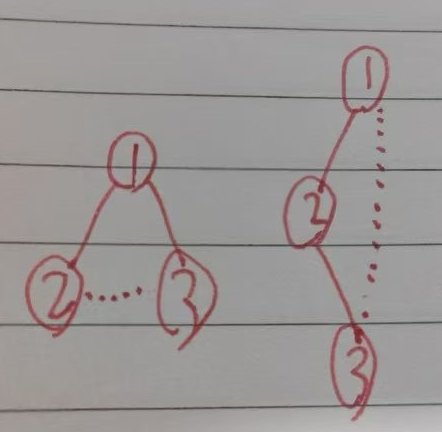
按照题目描述实际添加的边只有以上两种，这里称之为横边与竖边，我们先求出在没有两条边的情况下的距离之和，观察可得，每经过一条横或竖边总距离之和便可减1，所以分别求这两条边的贡献，同时视情况，下面可以借助竖边快速的向上跳跃，并且任意一个点若要通过除其父节点的子树外其他节点必然走竖边，在这种情况下我们可以直接计算此条竖边的贡献，并且动态的将此点看作已经向上跳跃到其父节点的父节点，在整个树中，向上跳跃到同一个节点的所有点去往除子树外所有节点均为同一种情况，所以可以使用递归对跳跃的节点进行统计，并同时计算此子树内边的竖边与横边的贡献值，进行树形操作。

所以两总边贡献统计操作，一条由a向上到c的竖边贡献为跳跃到a的节点数与除a的父节点的子树所有节点外的节点数相乘，此条竖边统计完，节点可进行跳跃操作并统计，一个节点a之下所有直接相连的子节点之间的横边便是任意一个子节点的跳跃节点数与所有子节点的跳跃子节点数减去当前子节点的跳跃子节点数。 总体思想为以竖边为主将节点动态的看待，由下至上进行树形操作。

代码

C++

#include <bits/stdc++.h>
#include <cstring>
using namespace std;
typedef long long ll;
const int N=200010;
ll n;
ll h[N],ne[N*2],e[N*2],idx;
ll dp[N],sum[N],tiao[N],tt[N],ans;
void add(int a,int b)
{
    e[idx]=b;
    ne[idx]=h[a];
    h[a]=idx++;
}
void dfs_zong(int u,int fa)//计算无加边情况下的距离总和
{
    sum[u]=1;
    tiao[u]=1;
    for(int i=h[u];i!=-1;i=ne[i])
    {
        int j=e[i];
        if(j==fa)continue;
        dfs_zong(j,u);
        sum[u]+=sum[j];
        dp[u]+=dp[j]+(n-sum[j])*sum[j]*2;
        if(u!=1)
        {
            tiao[fa]+=tiao[j];//动态计算跳跃节点数
        }
        tt[u]+=tiao[j];//此为计算该节点下直接相连的子节点跳跃节点数总和
    }
}
void dfs_jian(int u,int fa)
{
    for(int i=h[u];i!=-1;i=ne[i])
    {
        int j=e[i];
        if(j==fa)continue;
        dfs_jian(j,u);
        ans-=tiao[j]*(tt[u]-tiao[j]);//此为计算此节点下横边的贡献
        if(u!=1)
        {ans-=tiao[j]*(n-sum[u])*2;}//计算以此节点为中间节点的竖边的贡献，两倍是因为来回都算
    }
}
int main()
{
    cin>>n;
    memset(h,-1,sizeof(h));
    for(int i=0;i<n-1;i++)
    {
        int a,b;
        cin>>a>>b;
        add(a,b);
        add(b,a);
    }
    dfs_zong(1,-1);
    ans=dp[1];
    dfs_jian(1,-1);
    cout<<ans<<endl;
}

python

from collections import defaultdict

N = 200010
h = [-1] * N
ne = [0] * (N * 2)
e = [0] * (N * 2)
idx = 0
dp = [0] * N
sum = [0] * N
tiao = [0] * N
tt = [0] * N
ans = 0
n = int(input())

def add(a, b):
    global idx
    e[idx] = b
    ne[idx] = h[a]
    h[a] = idx
    idx += 1

def dfs_zong(u, fa):
    sum[u] = 1
    tiao[u] = 1
    i=h[u]
    while i!=-1:
        j = e[i]
        if j == fa:
            i=ne[i]
            continue
        dfs_zong(j, u)
        sum[u] += sum[j]
        dp[u] += dp[j] + (n - sum[j]) * sum[j] * 2
        if u != 1:
            tiao[fa] += tiao[j]
        tt[u] += tiao[j]
        i=ne[i]

def dfs_jian(u, fa):
    global ans
    i=h[u]
    while i!=-1:
        j = e[i]
        if j == fa:
            i=ne[i]
            continue
        dfs_jian(j, u)
        ans -= tiao[j] * (tt[u] - tiao[j])
        if u != 1:
            ans -= tiao[j] * (n - sum[u]) * 2
        i=ne[i]
for _ in range(n-1):
    a, b = map(int,input().split(' '))
    add(a, b)
    add(b, a)
dfs_zong(1, -1)
ans = dp[1]
dfs_jian(1, -1)
print(ans)

java

import java.util.*;

public class Main {
    static final int N = 200010;
    static long n;
    static long[] h = new long[N];
    static long[] ne = new long[N * 2];
    static long[] e = new long[N * 2];
    static long idx;
    static long[] dp = new long[N];
    static long[] sum = new long[N];
    static long[] tiao = new long[N];
    static long[] tt = new long[N];
    static long ans;

    public static void add(int a, int b) {
        e[(int)idx] = b;
        ne[(int)idx] = h[a];
        h[a] = idx++;
    }

    public static void dfs_zong(int u, int fa) {
        sum[u] = 1;
        tiao[u] = 1;
        for (int i = (int)h[u]; i != -1; i = (int)ne[i]) {
            int j = (int)e[i];
            if (j == fa) continue;
            dfs_zong(j, u);
            sum[u] += sum[j];
            dp[u] += dp[j] + (n - sum[j]) * sum[j] * 2;
            if (u != 1) {
                tiao[fa] += tiao[j];
            }
            tt[u] += tiao[j];
        }
    }

    public static void dfs_jian(int u, int fa) {
        for (int i = (int)h[u]; i != -1; i = (int)ne[i]) {
            int j = (int)e[i];
            if (j == fa) continue;
            dfs_jian(j, u);
            ans -= tiao[j] * (tt[u] - tiao[j]);
            if (u != 1) {
                ans -= tiao[j] * (n - sum[u]) * 2;
            }
        }
    }

    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        n = scanner.nextLong();
        Arrays.fill(h, -1);

        for (int i = 0; i < n - 1; i++) {
            int a = scanner.nextInt();
            int b = scanner.nextInt();
            add(a, b);
            add(b, a);
        }

        dfs_zong(1, -1);
        ans = dp[1];
        dfs_jian(1, -1);
        System.out.println(ans);
    }
}

题目内容

小红有一颗$n$个点的树。如果树上存在一个点$w$，使得原始的树上存在边$(u,w)$和$(w,v)$，那么我们可以添加一条边$(u,v)$.

小红想知道，添加若干条边之后，树上任意两点之间的距离之和最少是多少。即求$\sum_{i=1}^{n}\sum_{j=1}^{n}dist(i,j)$ 。

输入描述

第一行输入一个整数$n(2≤n≤2✖10^5)$代表树上的点数。

此后$n-1$行，第$i$行输入两个整数$u_i$和 $u_i(1≤u_i,v_i≤n；u_i≠v_i)$表示树上第$i$条 $u_i和v_i$。保证树联通，没有重边。

输出描述

在一行输出一个整数，代表树上 距离之和的最小值

样例1

输入

5
1 2
1 3
2 4
2 5

输出

24

**说明 **

可以添加边为（1,4),(1,5),(2,3),(4,5) 加边之后，1号点到其他点的距离为[0,1,1]

2号点到其他点的距离为[1,0,1,1,1]

3号点到其他点的距离为

4号点到其他点的距离为

5号点到其他点的距离为

距离总和为24

样例2

输入

输出