思路

• 关键性质：对于权值集合的最小公倍数，若把每个数按素数分解 $w=\prod p^{e_p}$，则 LCM 对应每个素数的指数取最大值。由于 $w_i \le 100$，素数仅有 $25$ 个（不超过 $97$），各指数极小（如 $2$ 的最大指数为 $6$）。

• 路径查询：仅为根到 $x$ 的路径。用重链剖分将路径拆成 $O(\log n)$ 个链段。

• 数据结构：用一棵线段树，节点维护一个长度为 $25$ 的小数组，表示该区间所有黑色节点对每个素数的指数最大值（白色为全零）。

  • 翻转颜色 → 点更新（设为该点的指数向量或全零）。
  • 查询根到 $x$ → 若干区间查询，合并（逐素数取最大），最后计算

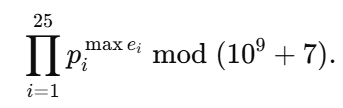
• 预处理：

  • 预分解 $1..100$ 的素数指数表；
  • 预计算每个素数在可能指数范围内的幂。

• 复杂度：每次操作 $O(25 \log n)$，可通过 $n,q \le 2\times 10^5$。

C++

#include <bits/stdc++.h>
using namespace std;

static const int MOD = 1000000007;

// 质数 <= 100
static const int PRIMES_ARR[] = {
    2,3,5,7,11,13,17,19,23,29,
    31,37,41,43,47,53,59,61,67,71,
    73,79,83,89,97
};
static const int P = 25;

int modmul(long long a, long long b){ return int((a*b)%MOD); }

// 预处理 1..100 的指数表
array<uint8_t, P> factExp[101];
// 预计算各素数的幂 prime^e
int maxExpPerPrime[P]; // 实际最大指数
int powTable[P][8];    // 8 已覆盖指数上限

// 树与 HLD
int n, q;
vector<vector<int>> g;
vector<int> w;
string color;

vector<int> parent_, depth_, heavy_, sz_;
vector<int> head_, pos_, invPos_;
int curPos = 0;

// 线段树，节点存 25 个字节（指数最大值）
struct SegTree {
    int n;
    vector<array<uint8_t, P>> t;

    SegTree() {}
    SegTree(int n): n(n) { t.assign(4*n+4, {}); }

    static inline void pull(array<uint8_t,P> &out, const array<uint8_t,P> &a, const array<uint8_t,P> &b) {
        for (int i=0;i<P;i++) out[i] = max(a[i], b[i]);
    }

    void build(int idx, int l, int r, const vector<array<uint8_t,P>> &base) {
        if (l==r) {
            t[idx] = base[l];
            return;
        }
        int mid=(l+r)>>1;
        build(idx<<1, l, mid, base);
        build(idx<<1|1, mid+1, r, base);
        pull(t[idx], t[idx<<1], t[idx<<1|1]);
    }

    void pointSet(int idx, int l, int r, int p, const array<uint8_t,P> &val) {
        if (l==r) {
            t[idx] = val;
            return;
        }
        int mid=(l+r)>>1;
        if (p<=mid) pointSet(idx<<1, l, mid, p, val);
        else pointSet(idx<<1|1, mid+1, r, p, val);
        pull(t[idx], t[idx<<1], t[idx<<1|1]);
    }

    void rangeQuery(int idx, int l, int r, int ql, int qr, array<uint8_t,P> &acc) {
        if (ql<=l && r<=qr) {
            for (int i=0;i<P;i++) acc[i] = max(acc[i], t[idx][i]);
            return;
        }
        int mid=(l+r)>>1;
        if (ql<=mid) rangeQuery(idx<<1, l, mid, ql, qr, acc);
        if (qr>mid) rangeQuery(idx<<1|1, mid+1, r, ql, qr, acc);
    }
} seg;

// 预处理素数分解指数
void prepareFactorExp() {
    for (int x=1;x<=100;x++) {
        int t=x;
        array<uint8_t,P> e{}; e.fill(0);
        for (int i=0;i<P;i++) {
            int p = PRIMES_ARR[i];
            int cnt=0;
            while (t%p==0){ t/=p; cnt++; }
            e[i] = (uint8_t)cnt;
        }
        factExp[x]=e;
    }
    // 最大指数与幂表
    memset(maxExpPerPrime, 0, sizeof(maxExpPerPrime));
    for (int x=1;x<=100;x++) {
        for (int i=0;i<P;i++) maxExpPerPrime[i] = max<int>(maxExpPerPrime[i], factExp[x][i]);
    }
    for (int i=0;i<P;i++) {
        powTable[i][0]=1;
        for (int e=1;e<8;e++) {
            long long v=1;
            for (int k=0;k<e;k++) v = (v*PRIMES_ARR[i])%MOD;
            powTable[i][e]=(int)v;
        }
    }
}

int dfs1(int u, int p){
    parent_[u]=p;
    depth_[u] = (p? depth_[p]+1:0);
    sz_[u]=1;
    int mx=0;
    for(int v: g[u]){
        if (v==p) continue;
        int s=dfs1(v,u);
        sz_[u]+=s;
        if (s>mx){ mx=s; heavy_[u]=v; }
    }
    return sz_[u];
}

void dfs2(int u, int h){
    head_[u]=h;
    pos_[u]=++curPos;
    invPos_[curPos]=u;
    if (heavy_[u]) dfs2(heavy_[u], h);
    for (int v: g[u]){
        if (v==parent_[u] || v==heavy_[u]) continue;
        dfs2(v, v);
    }
}

array<uint8_t,P> zeroVec(){
    array<uint8_t,P> z{}; z.fill(0); return z;
}

int main(){
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    cin>>n>>q;
    w.assign(n+1,0);
    for (int i=1;i<=n;i++) cin>>w[i];
    cin>>color;
    g.assign(n+1, {});
    for (int i=0;i<n-1;i++){
        int u,v; cin>>u>>v;
        g[u].push_back(v);
        g[v].push_back(u);
    }

    prepareFactorExp();

    parent_.assign(n+1,0);
    depth_.assign(n+1,0);
    heavy_.assign(n+1,0);
    sz_.assign(n+1,0);
    head_.assign(n+1,0);
    pos_.assign(n+1,0);
    invPos_.assign(n+1,0);
    curPos=0;

    dfs1(1,0);
    dfs2(1,1);

    vector<array<uint8_t,P>> base(n+1);
    for (int i=1;i<=n;i++){
        int u = invPos_[i];
        if (color[u-1]=='B') base[i]=factExp[w[u]];
        else base[i]=zeroVec();
    }

    seg = SegTree(n);
    seg.build(1,1,n,base);

    auto queryPath = [&](int u){
        array<uint8_t,P> acc{}; acc.fill(0);
        int v=1;
        while (head_[u]!=head_[v]) {
            seg.rangeQuery(1,1,n,pos_[head_[u]], pos_[u], acc);
            u=parent_[head_[u]];
        }
        seg.rangeQuery(1,1,n,pos_[v], pos_[u], acc);
        return acc;
    };

    auto applyToggle = [&](int x){
        array<uint8_t,P> val;
        if (color[x-1]=='B'){ // turn to white
            color[x-1]='W';
            val = zeroVec();
        }else{ // turn to black
            color[x-1]='B';
            val = factExp[w[x]];
        }
        seg.pointSet(1,1,n,pos_[x], val);
    };

    while(q--){
        int t,x; cin>>t>>x;
        if (t==1){
            applyToggle(x);
        }else{
            auto acc = queryPath(x);
            long long ans=1;
            for (int i=0;i<P;i++){
                int e = acc[i];
                ans = (ans * powTable[i][e]) % MOD;
            }
            cout<<ans<<"\n";
        }
    }
    return 0;
}

Python

import sys
sys.setrecursionlimit(1 << 25)

MOD = 10**9 + 7
PRIMES = [2,3,5,7,11,13,17,19,23,29,
          31,37,41,43,47,53,59,61,67,71,
          73,79,83,89,97]
P = len(PRIMES)

def build_fact():
    fact = [[0]*P for _ in range(101)]
    for x in range(1, 101):
        t = x
        for i, p in enumerate(PRIMES):
            cnt = 0
            while t % p == 0:
                t //= p
                cnt += 1
            fact[x][i] = cnt
    maxe = [0]*P
    for x in range(1, 101):
        for i in range(P):
            if fact[x][i] > maxe[i]:
                maxe[i] = fact[x][i]
    powtab = [[1]*8 for _ in range(P)]
    for i, p in enumerate(PRIMES):
        for e in range(1, 8):
            v = 1
            for _ in range(e):
                v = (v*p) % MOD
            powtab[i][e] = v
    return fact, maxe, powtab

def main():
    data = sys.stdin.read().strip().split()
    it = iter(data)
    n = int(next(it)); q = int(next(it))
    w = [0]*(n+1)
    for i in range(1, n+1):
        w[i] = int(next(it))
    color_s = list(next(it).strip())

    g = [[] for _ in range(n+1)]
    for _ in range(n-1):
        u = int(next(it)); v = int(next(it))
        g[u].append(v); g[v].append(u)

    fact, maxe, powtab = build_fact()

    parent = [0]*(n+1)
    depth = [0]*(n+1)
    sz = [0]*(n+1)
    heavy = [0]*(n+1)

    def dfs1(u, p):
        parent[u] = p
        depth[u] = 0 if p == 0 else depth[p] + 1
        sz[u] = 1
        mx = 0
        for v in g[u]:
            if v == p: continue
            dfs1(v, u)
            sz[u] += sz[v]
            if sz[v] > mx:
                mx = sz[v]
                heavy[u] = v

    head = [0]*(n+1)
    pos = [0]*(n+1)
    invpos = [0]*(n+1)
    cur = 0
    def dfs2(u, h):
        nonlocal cur
        head[u] = h
        cur += 1
        pos[u] = cur
        invpos[cur] = u
        if heavy[u]:
            dfs2(heavy[u], h)
        for v in g[u]:
            if v == parent[u] or v == heavy[u]: continue
            dfs2(v, v)

    dfs1(1,0)
    dfs2(1,1)

    # 线段树：扁平 bytearray，节点 idx 的起始偏移为 idx*P
    size = 4*n + 5
    seg = bytearray(size * P)

    def set_node(idx, vec):  # vec: list[int] 长度 P
        off = idx * P
        for i in range(P):
            seg[off+i] = vec[i]

    def pull(idx):
        off = idx * P
        l = (idx<<1)*P
        r = (idx<<1|1)*P
        for i in range(P):
            a = seg[l+i]; b = seg[r+i]
            seg[off+i] = a if a>=b else b

    def build(idx, l, r):
        if l == r:
            u = invpos[l]
            if color_s[u-1] == 'B':
                vec = fact[w[u]]
            else:
                vec = [0]*P
            set_node(idx, vec)
            return
        m = (l+r)//2
        build(idx<<1, l, m)
        build(idx<<1|1, m+1, r)
        pull(idx)

    def point_set(idx, l, r, pidx, vec):
        if l == r:
            set_node(idx, vec)
            return
        m = (l+r)//2
        if pidx <= m:
            point_set(idx<<1, l, m, pidx, vec)
        else:
            point_set(idx<<1|1, m+1, r, pidx, vec)
        pull(idx)

    def range_query_into(idx, l, r, ql, qr, acc):  # acc: list[int] 长度 P
        if ql <= l and r <= qr:
            off = idx * P
            for i in range(P):
                v = seg[off+i]
                if v > acc[i]: acc[i] = v
            return
        m = (l+r)//2
        if ql <= m: range_query_into(idx<<1, l, m, ql, qr, acc)
        if qr > m:  range_query_into(idx<<1|1, m+1, r, ql, qr, acc)

    build(1,1,n)

    out_lines = []
    for _ in range(q):
        t = int(next(it)); x = int(next(it))
        if t == 1:
            # 翻转
            if color_s[x-1] == 'B':
                color_s[x-1] = 'W'
                vec = [0]*P
            else:
                color_s[x-1] = 'B'
                vec = fact[w[x]]
            point_set(1,1,n,pos[x], vec)
        else:
            # 查询根到 x
            acc = [0]*P
            u = x
            v = 1
            while head[u] != head[v]:
                l = pos[head[u]]; r = pos[u]
                range_query_into(1,1,n,l,r,acc)
                u = parent[head[u]]
            l = pos[v]; r = pos[u]
            range_query_into(1,1,n,l,r,acc)
            ans = 1
            for i in range(P):
                e = acc[i]
                ans = (ans * powtab[i][e]) % MOD
            out_lines.append(str(ans))
    sys.stdout.write("\n".join(out_lines))

if __name__ == "__main__":
    main()

Java

import java.io.*;
import java.util.*;

public class Main {
    static final int MOD = 1_000_000_007;
    static final int[] PRIMES = {
        2,3,5,7,11,13,17,19,23,29,
        31,37,41,43,47,53,59,61,67,71,
        73,79,83,89,97
    };
    static final int P = 25;

    static int[][] fact = new int[101][P];
    static int[][] powtab = new int[P][8];

    static void prepare() {
        for (int x=1;x<=100;x++) {
            int t=x;
            for (int i=0;i<P;i++){
                int p = PRIMES[i], cnt=0;
                while (t%p==0){ t/=p; cnt++; }
                fact[x][i]=cnt;
            }
        }
        for (int i=0;i<P;i++){
            powtab[i][0]=1;
            for (int e=1;e<8;e++){
                long v=1;
                for (int k=0;k<e;k++) v=(v*PRIMES[i])%MOD;
                powtab[i][e]=(int)v;
            }
        }
    }

    static class FastScanner {
        final InputStream in;
        final byte[] buffer = new byte[1<<16];
        int ptr=0, len=0;
        FastScanner(InputStream is){ in=is; }
        int read() throws IOException {
            if (ptr>=len){ len=in.read(buffer); ptr=0; if (len<=0) return -1; }
            return buffer[ptr++];
        }
        String next() throws IOException {
            StringBuilder sb = new StringBuilder();
            int c;
            while ((c=read())!=-1 && c<=32);
            if (c==-1) return null;
            do { sb.append((char)c); } while ((c=read())!=-1 && c>32);
            return sb.toString();
        }
        int nextInt() throws IOException { return Integer.parseInt(next()); }
    }

    static int n, q;
    static ArrayList<Integer>[] g;
    static int[] w;
    static char[] color;

    static int[] parent, depth, sz, heavy, head, pos, invpos;
    static int cur;

    static class SegTree {
        int n;
        byte[] seg; // size: (4*n+4)*P

        SegTree(int n){
            this.n=n;
            seg = new byte[(4*n+5)*P];
        }
        void setNode(int idx, int[] vec){
            int off = idx*P;
            for (int i=0;i<P;i++) seg[off+i] = (byte)vec[i];
        }
        void setNodeZero(int idx){
            int off = idx*P;
            for (int i=0;i<P;i++) seg[off+i]=0;
        }
        void pull(int idx){
            int off = idx*P;
            int l = (idx<<1)*P, r=(idx<<1|1)*P;
            for (int i=0;i<P;i++){
                byte a=seg[l+i], b=seg[r+i];
                seg[off+i] = (a>=b? a:b);
            }
        }
        void build(int idx, int l, int r){
            if (l==r){
                int u = invpos[l];
                if (color[u-1]=='B') setNode(idx, fact[w[u]]);
                else setNodeZero(idx);
                return;
            }
            int m=(l+r)>>1;
            build(idx<<1,l,m);
            build(idx<<1|1,m+1,r);
            pull(idx);
        }
        void pointSet(int idx, int l, int r, int p, int[] vec, boolean zero){
            if (l==r){
                if (zero) setNodeZero(idx);
                else setNode(idx, vec);
                return;
            }
            int m=(l+r)>>1;
            if (p<=m) pointSet(idx<<1,l,m,p,vec,zero);
            else pointSet(idx<<1|1,m+1,r,p,vec,zero);
            pull(idx);
        }
        void rangeQueryInto(int idx, int l, int r, int ql, int qr, byte[] acc){
            if (ql<=l && r<=qr){
                int off = idx*P;
                for (int i=0;i<P;i++){
                    byte v = seg[off+i];
                    if (v>acc[i]) acc[i]=v;
                }
                return;
            }
            int m=(l+r)>>1;
            if (ql<=m) rangeQueryInto(idx<<1,l,m,ql,qr,acc);
            if (qr>m) rangeQueryInto(idx<<1|1,m+1,r,ql,qr,acc);
        }
    }

    static void dfs1(int u, int p){
        parent[u]=p;
        depth[u]=(p==0?0:depth[p]+1);
        sz[u]=1;
        int mx=0;
        for (int v: g[u]){
            if (v==p) continue;
            dfs1(v,u);
            sz[u]+=sz[v];
            if (sz[v]>mx){ mx=sz[v]; heavy[u]=v; }
        }
    }
    static void dfs2(int u, int h){
        head[u]=h;
        pos[u]=++cur;
        invpos[cur]=u;
        if (heavy[u]!=0) dfs2(heavy[u], h);
        for (int v: g[u]){
            if (v==parent[u] || v==heavy[u]) continue;
            dfs2(v, v);
        }
    }

    public static void main(String[] args) throws Exception {
        prepare();
        FastScanner fs = new FastScanner(System.in);
        n = Integer.parseInt(fs.next());
        q = Integer.parseInt(fs.next());

        w = new int[n+1];
        for (int i=1;i<=n;i++) w[i]=Integer.parseInt(fs.next());
        color = fs.next().toCharArray();

        g = new ArrayList[n+1];
        for (int i=0;i<=n;i++) g[i]=new ArrayList<>();
        for (int i=0;i<n-1;i++){
            int u = Integer.parseInt(fs.next());
            int v = Integer.parseInt(fs.next());
            g[u].add(v); g[v].add(u);
        }

        parent=new int[n+1];
        depth=new int[n+1];
        sz=new int[n+1];
        heavy=new int[n+1];
        head=new int[n+1];
        pos=new int[n+1];
        invpos=new int[n+1];
        cur=0;

        dfs1(1,0);
        dfs2(1,1);

        SegTree st = new SegTree(n);
        st.build(1,1,n);

        StringBuilder out = new StringBuilder();
        for (int i=0;i<q;i++){
            int t = Integer.parseInt(fs.next());
            int x = Integer.parseInt(fs.next());
            if (t==1){
                if (color[x-1]=='B'){
                    color[x-1]='W';
                    st.pointSet(1,1,n,pos[x], null, true);
                }else{
                    color[x-1]='B';
                    st.pointSet(1,1,n,pos[x], fact[w[x]], false);
                }
            }else{
                byte[] acc = new byte[P];
                int u=x, v=1;
                while (head[u]!=head[v]){
                    st.rangeQueryInto(1,1,n,pos[head[u]], pos[u], acc);
                    u = parent[head[u]];
                }
                st.rangeQueryInto(1,1,n,pos[v], pos[u], acc);
                long ans=1;
                for (int pi=0;pi<P;pi++){
                    int e = acc[pi] & 0xFF;
                    ans = (ans * powtab[pi][e]) % MOD;
                }
                out.append(ans).append('\n');
            }
        }
        System.out.print(out.toString());
    }
}

题目内容

给定一棵以节点 $1$ 为根的有 $n$ 个节点的树，每个节点 $i$ 有一个正整数权值 $w_i$ ，初始被涂成黑色或白色。你需要支持以下两种操作；

1.翻转节点 $x$ 的颜色(黑色变白色，自色变黑色)；

2.查询从根节点 $1$ 到节点 $x$ 的路径上所有黑色节点的权值的最小公倍数(若路径上无黑色节点，则记为 $1$ )

【名词解释】

最小公倍数：最小公倍数是能够被给定整数集合中每个整数整除的最小正整数，记为 $Icm$ 。

输入描述

第一行输入两个整数 $n$ 和 $q(1≦n,q≦2×10^5)$，分别表示树的节点数量和操作数量。

第二行输入 $n$ 个整数 $w_1,w_2,...,w_n(1≦w_i≦100)$，分别表示节点 $1$ 到节点 $n$ 的权值。

第三行输入一个长度为 $n$ 、仅由字符 $B$ 和 $W$ 构成的字符串 $c$，其中 $c_1=B$ 表示节点 $i$ 初始化为黑色，$c_i=W$ 表示初始化为白色。

接下来 $n-1$ 行，每行输入两个整数 $u_i$ 和 $v_i(1≦u_i,v_i≦n;u_i≠v_i)$ ，表示一条连接节点 $u_i$ 和节点 $v_i$ 的无向边，保证这 $n$ 个节点构成一颗根为 $1$ 的树。

接下来 $q$ 行，每行输入两个整数 $t$ 和 $x(t∈{1,2},1≦x≦n)$ ，表示一次操作。

1.当 $t=1$ 时，执行翻转操作；

2.当 $t=1$ 时，执行查询操作。

输出描述

对于每次查询操作，在一行中输出一个整数，表示对应路径上黑色节点权值的最小公倍数对 $(10^9+7)$ 取模后的结果。

样例1

输入

5 5
2 3 4 5 6
BWBWB
1 2
1 3
3 4
3 5
2 4
1 3
2 4
1 1
2 5

输出

4
2
5

说明

在这个样例中，初始颜色为

• 节点 $1→B$ ；

• 节点 $2→W$ ；

• 节点 $3→B$ ；

• 节点 $4→W$ ；

• 节点 $5→B$ 。

第一条查询 $2$ $4$ ：路径 $1-3-4$ 上黑色节点为 $1,3$ ，权值分别为 $2,4$ ，$lcm(2,4)=4$，翻转节点 $3$ 后第二次查询 $2$ $4$ ；路径上仅剩节点 $1$ 为黑色，$lcm(2)=2$ ，再翻转节点 $1$ 后第三次查询 $2$ $5$ ；路径 $1-3-5$ 上仅有节点 $5$ 为黑色，$lcm(6)=6$ 。