题解

• 结论

  • 设数组为 $a_1,\dots,a_n$，最大值为 $M=\max(a_i)$，其二进制长度为 $L$（特别地，当 $M=0$ 时 $L=1$）。
  • 记按位与为 $A=\bigwedge_{i=1}^n a_i$，定义掩码 $mask=2^L-1$。
  • 使总和最大的最小初始 $x$ 为：

  

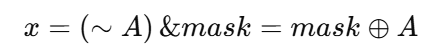
  • 数组可达到的最大总和为：$S_{\max}=\left(\sum_{i=1}^n a_i\right)+x$。

• 理由（按位独立，操作等价于“把 $x$ 的某些 $1$ 位转移到某个 $a_i$ 上”）

  • 考察某一比特位 $k$：若所有 $a_i$ 的该位均为 $1$（即该位在 $A$ 中为 $1$），则无法再提升这一位的数组总和；否则，若初始令 $x$ 的该位为 $1$，总和至多提升 $2^k$，且一定能通过在某次操作选择一个该位为 $0$ 的下标来实现这 $2^k$ 的提升。
  • 每一位最多提升一次，因此最大可增量正是所有“并非全为 $1$ 的位”的位权之和，等于 $mask\oplus A$ 的数值。
  • 要达到这一上界，初始应令这些位都在 $x$ 中为 $1$；反之若少选任一位，则对应的 $2^k$ 无法被创造出来，总和达不到最大。因此在达到最大总和的前提下，最小的 $x$ 唯一且为 $x=mask\oplus A$。
  • 位长约束通过 $mask=2^L-1$ 保证仅使用最低 $L$ 位（当 $M=0$ 时 $L=1$）。

C++

#include <bits/stdc++.h>
using namespace std;

int main() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr);
	int T;
	if (!(cin >> T)) return 0;
	while (T--) {
		int n;
		cin >> n;
		vector<int> a(n);
		long long sum = 0;
		int mx = 0;
		for (int i = 0; i < n; ++i) {
			cin >> a[i];
			sum += a[i];     // 累加数组和
			mx = max(mx, a[i]); // 记录最大值
		}
		// 计算二进制位长 L（当 mx=0 时，L=1）
		int L = (mx == 0) ? 1 : (32 - __builtin_clz(mx));
		long long mask = (L == 63 ? (LLONG_MAX) : ((1LL << L) - 1)); // 这里 L<=30，安全
		// 按位与 A
		int A = (1 << 30) - 1; // 30 位全 1
		for (int v : a) A &= v;
		long long x = (mask ^ (A & (int)mask)); // x = mask XOR A（仅保留低 L 位）
		long long ans = sum + x; // 最大和 = 原和 + x（x 的数值等于能增加的总位权）
		cout << ans << ' ' << x << '\n';
	}
	return 0;
}

Python

import sys

def bit_length_nonzero(x: int) -> int:
	# 返回正整数的二进制位长；x=0 时外部特殊处理
	return x.bit_length()

data = sys.stdin.read().strip().split()
it = iter(data)
T = int(next(it))
out_lines = []
for _ in range(T):
	n = int(next(it))
	a = [int(next(it)) for _ in range(n)]
	s = sum(a)  # 数组和
	mx = max(a) if a else 0
	L = 1 if mx == 0 else bit_length_nonzero(mx)
	mask = (1 << L) - 1  # 仅低 L 位
	A = (1 << 30) - 1
	for v in a:
		A &= v
	x = mask ^ (A & mask)  # x = (~A)&mask 等价于 mask XOR A 的低 L 位
	ans = s + x
	out_lines.append(f"{ans} {x}")

sys.stdout.write("\n".join(out_lines))

Java

import java.io.*;
import java.util.*;

public class Main {
	static class FastScanner {
		private final InputStream in;
		private final byte[] buffer = new byte[1 << 16];
		private int ptr = 0, len = 0;
		FastScanner(InputStream is) { in = is; }
		private int read() throws IOException {
			if (ptr >= len) {
				len = in.read(buffer);
				ptr = 0;
				if (len <= 0) return -1;
			}
			return buffer[ptr++];
		}
		int nextInt() throws IOException {
			int c, sgn = 1, x = 0;
			do { c = read(); } while (c <= ' ' && c != -1);
			if (c == '-') { sgn = -1; c = read(); }
			while (c > ' ') {
				x = x * 10 + (c - '0');
				c = read();
			}
			return x * sgn;
		}
	}
	public static void main(String[] args) throws Exception {
		FastScanner fs = new FastScanner(System.in);
		StringBuilder sb = new StringBuilder();
		int T;
		try { T = fs.nextInt(); } catch (Exception e) { return; }
		while (T-- > 0) {
			int n = fs.nextInt();
			int[] a = new int[n];
			long sum = 0;
			int mx = 0;
			for (int i = 0; i < n; i++) {
				a[i] = fs.nextInt();
				sum += a[i];    // 累加数组和
				if (a[i] > mx) mx = a[i]; // 最大值
			}
			// 计算二进制位长 L（当 mx=0 时 L=1）
			int L = (mx == 0) ? 1 : (32 - Integer.numberOfLeadingZeros(mx));
			long mask = (1L << L) - 1; // 仅低 L 位
			int A = (1 << 30) - 1;     // 30 位全 1
			for (int v : a) A &= v;    // 按位与
			long x = mask ^ (A & (int)mask); // x = (~A)&mask 等价形式
			long ans = sum + x;        // 最大和
			sb.append(ans).append(' ').append(x).append('\n');
		}
		System.out.print(sb.toString());
	}
}

题目内容

小美有一个长度为 $n$ 的数组 {$a_1,a_2,...,a_n$} ，他希望构造一个非负整数 $x$ ， 满足 $x$ 的二进制位数不超过数组中最大值的二进制位数(特别的 $0$ 二进制位数为 $1$ )。

随后，可对数组 $a$ 重复进行以下操作，以使所有元素的总和最大：

• 选择一个下标 $i$ ，同时将 $a_i$ 修改为 $a_i$ $or$ $x$ ，将 $x$ 修改为 $a_i$ $and$ $x$ 。

在使元素总和达到最大值的前提下，要求所有操作前初始的 $x$ 尽可能小。请输出最大总和及对应的最小 $x$ 。

按位或：$or$ 表示按位或运算，即对两个整数的二进制表示的每一位进行逻辑或操作。

按位与：$and$ 表示按位与运算，即对两个整数的二进制表的每一位进行逻辑与操作。

输入描述

每个测试文件均包含多组测试数据。

第一行输入一个整数 $T(1≦T≦1000)$ ，代表数据组数；

对于每组测试数据，输入如下：

第一行输入一个整数 $n(1 ≦ n≦ 500)$ ，表示数组的长度；

第二行输入 $n$ 个整数 $a_1, a_2,...,a_n(0 ≦ a_i< 2^{30})$，表示数组 $a$ 的元素。

输出描述

对于每组测试数据，新起一行，输出两个整数，用空格分隔：第一个整数为数组可以达到的最大总和；第二个整数为在达到最大总和的前提下初始最小的 $x$ 。

样例1

输入

2
2
3 3
3
1 2 3

输出

6 0
9 3