思路总览

核心目标：在动态切换红点的同时，高效回答“到所有红点距离之和”。直接维护会超时，因此使用点分治配合分层距离与分组前缀量维护。

关键记号

• 用点分治把树分成若干层重心。对每个原树节点 $u$，记录它到每一层重心的距离序列：

  

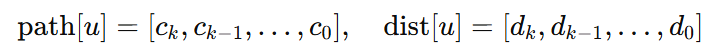
  其中 $c_i$ 是某一层的重心（从“最深”那层到“最顶”那层），$d_i = \text{dist}(u, c_i)$。

• 对每个重心 $c$ 维护两类量：

  1. 全体红点在 $c$ 处的聚合量

  

  2. “沿着某个子分治方向”的子聚合量（用“下层重心”作键）

  

  这里的 $p$ 是 $c$ 的下层重心（即点分治树上 $c$ 的某个孩子），它唯一代表“从 $c$ 走向某个连通分量的方向”。

更新（切换红点 $u$，令 $Delta = +1$ 表示变红、$Delta = -1$ 表示变非红）

沿 $u$ 的重心链自下而上遍历： 设当前重心为 $c$，且与之下一层的重心为 $p$（若不存在则忽略第二项），并记 $d=\text{dist}(u,c)$。 做

若存在$p$，再做

查询（求 $S_v$）

同样沿 $v$ 的重心链自下而上遍历： 设当前重心为 $c$，下层重心为 $p$（若不存在忽略扣除项），$d=\text{dist}(v,c)$。 总和累加：

为避免把“与 $v$ 同处 $c$ 的同一子方向”的红点重复计入，需要扣除：

处理完整条重心链后，所得即为 $S_v$。

C++

#include <bits/stdc++.h>
using namespace std;

// --------------- 全局结构 ---------------
struct Edge { int to; int w; };
const int MAXN = 200000 + 5;

int n, q;
vector<Edge> g[MAXN];

// 点分治需要的标记与数据
bool removed_[MAXN];
int sz[MAXN];
int cpar[MAXN]; // 点分治树上的父重心（根为 -1）

// 对每个原树节点：其重心链（从上到下/从顶到底存储），以及到这些重心的距离
vector<int> cpath[MAXN];
vector<long long> cdist[MAXN];

// 统计量
long long totCnt[MAXN], totDistSum[MAXN];
// 每个重心 c 的子方向统计：使用 unordered_map<下层重心, 值>
unordered_map<int, long long> subCnt[MAXN], subDistSum[MAXN];

// 初始红点状态
vector<int> initRed;
vector<char> isRed;

// --------------- 点分治（递归版） ---------------
int calcSize(int u, int p) {
    sz[u] = 1;
    for (auto e : g[u]) {
        int v = e.to;
        if (v == p || removed_[v]) continue;
        sz[u] += calcSize(v, u);
    }
    return sz[u];
}

int findCentroid(int u, int p, int tot) {
    for (auto e : g[u]) {
        int v = e.to;
        if (v == p || removed_[v]) continue;
        if (sz[v] > tot / 2) return findCentroid(v, u, tot);
    }
    return u;
}

void collect(int u, int p, int cen, long long dist) {
    // 把 cen 挂到 u 的重心链末尾，并记录距离
    cpath[u].push_back(cen);
    cdist[u].push_back(dist);
    for (auto e : g[u]) {
        int v = e.to;
        if (v == p || removed_[v]) continue;
        collect(v, u, cen, dist + e.w);
    }
}

void decompose(int entry, int parent) {
    int tot = calcSize(entry, -1);
    int cen = findCentroid(entry, -1, tot);
    // 先收集 cen 覆盖的本组件所有点到 cen 的距离
    collect(cen, -1, cen, 0);
    cpar[cen] = parent;
    removed_[cen] = true;
    // 递归处理每个未移除的相邻分量
    for (auto e : g[cen]) {
        int v = e.to;
        if (!removed_[v]) {
            decompose(v, cen);
        }
    }
    // 不必恢复 removed_[cen]
}

// --------------- 维护（切换 / 查询） ---------------
void apply_update(int u, int delta) {
    // delta = +1 表示设为红点；-1 表示设为非红点
    int prev = -1;
    int m = (int)cpath[u].size();
    for (int i = m - 1; i >= 0; --i) {
        int c = cpath[u][i];
        long long d = cdist[u][i];
        totCnt[c] += delta;
        totDistSum[c] += 1LL * delta * d;
        if (prev != -1) {
            subCnt[c][prev] += delta;
            subDistSum[c][prev] += 1LL * delta * d;
        }
        prev = c;
    }
}

long long query_sum(int u) {
    long long ans = 0;
    int prev = -1;
    int m = (int)cpath[u].size();
    for (int i = m - 1; i >= 0; --i) {
        int c = cpath[u][i];
        long long d = cdist[u][i];
        ans += totDistSum[c] + totCnt[c] * d;
        if (prev != -1) {
            auto it1 = subDistSum[c].find(prev);
            auto it2 = subCnt[c].find(prev);
            long long sd = (it1 == subDistSum[c].end() ? 0LL : it1->second);
            long long sc = (it2 == subCnt[c].end() ? 0LL : it2->second);
            ans -= sd + sc * d;
        }
        prev = c;
    }
    return ans;
}

// --------------- 主过程 ---------------
int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    cin >> n >> q;
    initRed.resize(n + 1);
    isRed.assign(n + 1, 0);
    for (int i = 1; i <= n; ++i) {
        cin >> initRed[i];
        isRed[i] = (initRed[i] ? 1 : 0);
    }
    for (int i = 0; i < n - 1; ++i) {
        int u, v, w;
        cin >> u >> v >> w;
        g[u].push_back({v, w});
        g[v].push_back({u, w});
    }

    // 点分治建树 + 预处理各点到各层重心距离
    decompose(1, -1);

    // 根据初始红点批量加入
    for (int i = 1; i <= n; ++i) {
        if (isRed[i]) apply_update(i, +1);
    }

    // 在线处理操作
    for (int i = 0; i < q; ++i) {
        int t, v;
        cin >> t >> v;
        if (t == 1) {
            if (isRed[v]) {
                apply_update(v, -1);
                isRed[v] = 0;
            } else {
                apply_update(v, +1);
                isRed[v] = 1;
            }
        } else {
            cout << query_sum(v) << "\n";
        }
    }
    return 0;
}

Python

import sys
sys.setrecursionlimit(1 << 25)
data = sys.stdin.buffer.read().split()
it = iter(data)
def ni(): return int(next(it))

n, q = ni(), ni()
init = [0]*(n+1)
is_red = [0]*(n+1)
for i in range(1, n+1):
    init[i] = ni()
    is_red[i] = 1 if init[i] == 1 else 0

g = [[] for _ in range(n+1)]
for _ in range(n-1):
    u, v, w = ni(), ni(), ni()
    g[u].append((v, w))
    g[v].append((u, w))

removed = [False]*(n+1)
sz = [0]*(n+1)
cpar = [-1]*(n+1)

# 每个点到各层重心的链及距离（从上到下存，使用时倒序遍历）
cpath = [[] for _ in range(n+1)]
cdist = [[] for _ in range(n+1)]

totCnt = [0]*(n+1)
totDist = [0]*(n+1)
from collections import defaultdict
subCnt = [defaultdict(int) for _ in range(n+1)]
subDist = [defaultdict(int) for _ in range(n+1)]

def calc_size(u, p):
    sz[u] = 1
    for v, w in g[u]:
        if v == p or removed[v]:
            continue
        calc_size(v, u)
        sz[u] += sz[v]

def find_centroid(u, p, tot):
    for v, w in g[u]:
        if v == p or removed[v]:
            continue
        if sz[v] > tot // 2:
            return find_centroid(v, u, tot)
    return u

def collect(u, p, cen, dist):
    # 把当前重心 cen 附加到 u 的重心链
    cpath[u].append(cen)
    cdist[u].append(dist)
    for v, w in g[u]:
        if v == p or removed[v]:
            continue
        collect(v, u, cen, dist + w)

def decompose(entry, parent):
    calc_size(entry, -1)
    cen = find_centroid(entry, -1, sz[entry])
    # 先收集距离
    collect(cen, -1, cen, 0)
    cpar[cen] = parent
    removed[cen] = True
    for v, w in g[cen]:
        if not removed[v]:
            decompose(v, cen)

def apply_update(u, delta):
    prev = -1
    m = len(cpath[u])
    for i in range(m-1, -1, -1):
        c = cpath[u][i]
        d = cdist[u][i]
        totCnt[c] += delta
        totDist[c] += delta * d
        if prev != -1:
            subCnt[c][prev] += delta
            subDist[c][prev] += delta * d
        prev = c

def query_sum(u):
    ans = 0
    prev = -1
    m = len(cpath[u])
    for i in range(m-1, -1, -1):
        c = cpath[u][i]
        d = cdist[u][i]
        ans += totDist[c] + totCnt[c] * d
        if prev != -1:
            ans -= subDist[c].get(prev, 0) + subCnt[c].get(prev, 0) * d
        prev = c
    return ans

# 建立点分治 + 初始装载
decompose(1, -1)
for i in range(1, n+1):
    if is_red[i]:
        apply_update(i, +1)

out_lines = []
for _ in range(q):
    t, v = ni(), ni()
    if t == 1:
        if is_red[v]:
            apply_update(v, -1)
            is_red[v] = 0
        else:
            apply_update(v, +1)
            is_red[v] = 1
    else:
        out_lines.append(str(query_sum(v)))

sys.stdout.write("\n".join(out_lines))

Java

import java.io.*;
import java.util.*;

// 为了避免极端递归深度导致的栈溢出，主逻辑放到大栈线程里。
public class Main {
    static class FastScanner {
        private final InputStream in;
        private final byte[] buffer = new byte[1 << 16];
        private int ptr = 0, len = 0;
        FastScanner(InputStream is) { in = is; }
        private int read() throws IOException {
            if (ptr >= len) {
                len = in.read(buffer);
                ptr = 0;
                if (len <= 0) return -1;
            }
            return buffer[ptr++];
        }
        int nextInt() throws IOException {
            int c, sgn = 1, x = 0;
            do { c = read(); } while (c <= 32);
            if (c == '-') { sgn = -1; c = read(); }
            while (c > 32) {
                x = x * 10 + (c - '0');
                c = read();
            }
            return x * sgn;
        }
    }

    static class Edge { int to, w; Edge(int t,int w){this.to=t; this.w=w;} }

    static int n, q;
    static ArrayList<Edge>[] g;

    // 点分治
    static boolean[] removed;
    static int[] sz, cpar;

    // 每个点到各层重心的链（自上而下存，使用时倒序）
    static ArrayList<Integer>[] cpath;
    static ArrayList<Long>[] cdist;

    // 统计量
    static long[] totCnt, totDist;
    // 子方向统计：HashMap<下层重心, 值>
    @SuppressWarnings("unchecked")
    static HashMap<Integer, Long>[] subCnt, subDist;

    static int[] init;
    static boolean[] isRed;

    static void calcSize(int u, int p) {
        sz[u] = 1;
        for (Edge e : g[u]) {
            int v = e.to;
            if (v == p || removed[v]) continue;
            calcSize(v, u);
            sz[u] += sz[v];
        }
    }

    static int findCentroid(int u, int p, int tot) {
        for (Edge e : g[u]) {
            int v = e.to;
            if (v == p || removed[v]) continue;
            if (sz[v] > tot / 2) return findCentroid(v, u, tot);
        }
        return u;
    }

    static void collect(int u, int p, int cen, long dist) {
        cpath[u].add(cen);
        cdist[u].add(dist);
        for (Edge e : g[u]) {
            int v = e.to;
            if (v == p || removed[v]) continue;
            collect(v, u, cen, dist + e.w);
        }
    }

    static void decompose(int entry, int parent) {
        calcSize(entry, -1);
        int cen = findCentroid(entry, -1, sz[entry]);
        collect(cen, -1, cen, 0L);
        cpar[cen] = parent;
        removed[cen] = true;
        for (Edge e : g[cen]) {
            int v = e.to;
            if (!removed[v]) decompose(v, cen);
        }
    }

    static void applyUpdate(int u, int delta) {
        int prev = -1;
        int m = cpath[u].size();
        for (int i = m - 1; i >= 0; --i) {
            int c = cpath[u].get(i);
            long d = cdist[u].get(i);
            totCnt[c] += delta;
            totDist[c] += (long)delta * d;
            if (prev != -1) {
                subCnt[c].put(prev, subCnt[c].getOrDefault(prev, 0L) + delta);
                subDist[c].put(prev, subDist[c].getOrDefault(prev, 0L) + (long)delta * d);
            }
            prev = c;
        }
    }

    static long querySum(int u) {
        long ans = 0;
        int prev = -1;
        int m = cpath[u].size();
        for (int i = m - 1; i >= 0; --i) {
            int c = cpath[u].get(i);
            long d = cdist[u].get(i);
            ans += totDist[c] + totCnt[c] * d;
            if (prev != -1) {
                long sd = subDist[c].getOrDefault(prev, 0L);
                long sc = subCnt[c].getOrDefault(prev, 0L);
                ans -= sd + sc * d;
            }
            prev = c;
        }
        return ans;
    }

    public static void main(String[] args) throws Exception {
        new Thread(null, () -> {
            try {
                FastScanner fs = new FastScanner(System.in);
                n = fs.nextInt();
                q = fs.nextInt();
                init = new int[n+1];
                isRed = new boolean[n+1];

                g = new ArrayList[n+1];
                for (int i = 1; i <= n; ++i) g[i] = new ArrayList<>();
                for (int i = 1; i <= n; ++i) {
                    init[i] = fs.nextInt();
                    isRed[i] = init[i] == 1;
                }
                for (int i = 0; i < n-1; ++i) {
                    int u = fs.nextInt(), v = fs.nextInt(), w = fs.nextInt();
                    g[u].add(new Edge(v, w));
                    g[v].add(new Edge(u, w));
                }

                removed = new boolean[n+1];
                sz = new int[n+1];
                cpar = new int[n+1];
                Arrays.fill(cpar, -1);

                cpath = new ArrayList[n+1];
                cdist = new ArrayList[n+1];
                for (int i = 1; i <= n; ++i) {
                    cpath[i] = new ArrayList<>();
                    cdist[i] = new ArrayList<>();
                }

                totCnt = new long[n+1];
                totDist = new long[n+1];

                subCnt = new HashMap[n+1];
                subDist = new HashMap[n+1];
                for (int i = 1; i <= n; ++i) {
                    subCnt[i] = new HashMap<>();
                    subDist[i] = new HashMap<>();
                }

                // 建点分治 + 初始装载红点
                decompose(1, -1);
                for (int i = 1; i <= n; ++i) if (isRed[i]) applyUpdate(i, +1);

                StringBuilder out = new StringBuilder();
                for (int i = 0; i < q; ++i) {
                    int t = fs.nextInt(), v = fs.nextInt();
                    if (t == 1) {
                        if (isRed[v]) {
                            applyUpdate(v, -1);
                            isRed[v] = false;
                        } else {
                            applyUpdate(v, +1);
                            isRed[v] = true;
                        }
                    } else {
                        out.append(querySum(v)).append('\n');
                    }
                }
                System.out.print(out.toString());
            } catch (Exception e) {
                e.printStackTrace();
            }
        }, "big-stack", 1 << 26).start(); // 提高线程栈
    }
}

题目内容

给定一棵以节点 $1$ 为根的树，树上共有 $n$ 个节点，其中某些节点被标记为"红点"。每条边 $(u,v)$ 具有正整数权重 $w_{uv}$ 。

接下来有 $q$ 次操作，每次操作有两种类型：

1.切换节点 $v$ 的红点状态(若为红点则变为非红点，反之亦然)

2.查询节点 $v$ 到所有当前红点的带权距离之和 $S_v$ 。

请对所有查询操作输出对应结果。

【名词解释】：

• 带权距离：带权距离 指路径上所有边权的总和。

输入描述

第一行输入两个整数 $n,q(1 ≤ n,q≦ 2 ×10^5)$ ，分别表示节点数和操作数。

第二行输入 $n$ 个整数 $c_1,c_2,…,c_n ∈$ {$0,1$} ，其中 $c_i = 1$ 表示第 $i$ 个节点初始为红点，$c_i=0$ 表示非红点。

接下来 $n -1$ 行，每行输入三个整数 $u_i,v_i,w_i(1≤u_i,u_i≦n, u_i≠v_i,1≤w_i≤10^6)$ ，表示一条无向带权边。

随后 $q$ 行，每行输入两个整数 $t$ 和 $v(t ∈$ {$1,2$} $,1 ≦u≦ n)$，表示一次操作。

保证所有输入的边构成一棵树，并且至少存在一个操作 $2$ 。

输出描述

对于每个操作类型 $2$ ，输出一行整数，表示节点 $v$ 到所有当前红点的带权距离之和 $S_v$ 。

样例1

输入

5 5
1 0 1 0 1
1 2 1
1 3 2
3 4 3
3 5 4
2 1
2 2
1 3
2 2
2 2

输出

8
11
8
8

说明

在这个样例中：

初始红点为 {$1,3,5$} ;

操作 $2$ $1$ ：$S_1=0+2+6=8$ ；

操作 $2$ $2$ ：$S_2=1+3+7= 11$ ；

操作 $1$ $3$ ：切换节点 $3$ 为非红点，红点变为 {$1,5$} ；

操作 $2$ $2$ ：$S_2=1+7=8$ ；

操作 $2$ $2$ ：红点不变，$S_2 = 8$ 。