思路与证明

关键变换

设 $x$ 的二进制在 $20$ 位内，令集合 $S$ 为 $x$ 中为 $1$ 的位位置集合，$C$ 为其补集（即 $x$ 中为 $0$ 的位，数量记为 $m$）。 对任意候选数 $a$，要让与任意另一个 $a'$ 有 $a$ & $a'$=$x$，显然 $a$ 在 $S$ 上必须全为 $1$。于是可以写成

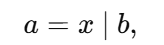
其中 $b$ 只能在 $C$ 的这些位上取 $0/1$，在 $S$ 上必须为 $0$。

对两个数 $a_i=x \vert b_i$ 与 $a_j=x \vert b_j$，

要使其等于 $x$，充要条件是

于是问题等价为：在 $m$ 位（即 $x$ 的 $0$ 位）上，选出尽可能多的两两按位与为 $0$ 的不同掩码 $b_i$。然后输出 $a_i=x \vert b_i$。

最优构造与上界

• 上界：在 $m$ 位中，如果我们选择的 $b_i$ 都两两无交（即两两按位与为 $0$），那么这些 $b_i$ 的所有$1$ 位互不重叠。记所有 $b_i$ 的 $1$ 位总数之和为$t$，显然 $t\le m$。 除了 $b=0$ 不消耗位以外，每加入一个非零 $b_i$ 至少消耗 $1$ 个可用位。因此最多能选 $m$ 个非零 $b$，再加上 $b=0$ 这一项，得到

  

• 下界（构造）：取一组 $b$ 为

  

  即 $0$ 和每个在 $C$ 中的单比特掩码。它们两两按位与为 $0$，恰好得到 $m+1$ 个不同的 $b$，于是

  

  达到上界，是最优解。

特别地，当 $x=2^{20}-1$ 时，$m=0$，最优 $k=1$。此时可以输出任意一个数（我们直接输出 $x$ 即可）。

C++

#include <bits/stdc++.h>
using namespace std;

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int T;
    if (!(cin >> T)) return 0;
    while (T--) {
        int x;
        cin >> x;
        vector<int> ans;
        // 先放入 x（对应 b=0）
        ans.push_back(x);
        // 对 0..19 位，若该位在 x 中为 0，则可以加入 x | (1<<p)
        for (int p = 0; p < 20; ++p) {
            if (((x >> p) & 1) == 0) {
                ans.push_back(x | (1 << p));
            }
        }
        // 输出
        cout << ans.size() << "\n";
        for (int i = 0; i < (int)ans.size(); ++i) {
            if (i) cout << ' ';
            cout << ans[i];
        }
        cout << "\n";
    }
    return 0;
}

Python

import sys

def solve():
    data = sys.stdin.read().strip().split()
    it = iter(data)
    T = int(next(it))
    out_lines = []
    for _ in range(T):
        x = int(next(it))
        ans = []
        # 先放入 x（对应 b=0）
        ans.append(x)
        # 遍历 0..19 位，x 为 0 的位各加入一个单比特
        for p in range(20):
            if ((x >> p) & 1) == 0:
                ans.append(x | (1 << p))
        out_lines.append(str(len(ans)))
        out_lines.append(" ".join(map(str, ans)))
    sys.stdout.write("\n".join(out_lines))

if __name__ == "__main__":
    solve()

Java

import java.io.*;
import java.util.*;

public class Main {
    public static void main(String[] args) throws Exception {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringBuilder out = new StringBuilder();
        int T = Integer.parseInt(br.readLine().trim());
        while (T-- > 0) {
            String line;
            // 读取可能带空行的输入
            do {
                line = br.readLine();
            } while (line != null && line.trim().isEmpty());
            int x = Integer.parseInt(line.trim());

            ArrayList<Integer> ans = new ArrayList<>();
            // 先放入 x（对应 b=0）
            ans.add(x);
            // 对 0..19 位，若该位在 x 中为 0，则加入 x | (1<<p)
            for (int p = 0; p < 20; ++p) {
                if (((x >> p) & 1) == 0) {
                    ans.add(x | (1 << p));
                }
            }
            // 输出
            out.append(ans.size()).append('\n');
            for (int i = 0; i < ans.size(); ++i) {
                if (i > 0) out.append(' ');
                out.append(ans.get(i));
            }
            out.append('\n');
        }
        System.out.print(out.toString());
    }
}

题目内容

小美有一个最喜欢的小于 $2^{20}$ 的非负整数 $x$ 。

我们称数组 $a$ 是 美丽的 ，当且仅当其满是以下所有条件：

• 数组 $a$ 中的每个元素都小于 $2^{20}$ 。

• 数组 $a$ 中 不包含 相同的数。

• 对于数组 $a$ 中任意两个处在不同位置的数 $a_i$ 和 $a_j$ ，都满足 $a_i$ & $a_j =x$，其中 & 为按位与运算。特别地，当数组长度为 $1$ 时，也视为满足此条件。

现在小美想让你帮他找到一个最长的美丽数组。如果存在多个最长的美丽数组，您可以输出任意一个，系统会自动判定是否正确。注意，自测运行功能可能因此返回错误结果，请自行检查答案正确性。

输入描述

每个测试文件均包含多组测试数据。一行输入一个整数 $T(1≤T≤500)$ 代表数据组数，每组测试数据描述如下：

输入一行一个整数 $x(0≤x<2^{20})$ ，表示小美最喜欢的非负整数。

输出描述

对于每组测试数据，先输出一行一个整数 $k(1≦k≦100)$，表示最长的美丽数组的长度。可以证明在本题的数据范围内，最长的美丽数组的长度不会超过 $100$ 。

接下来，在第二行输出 $k$ 个不同整数 $a_1,a_2,…,a_k(0≦a_i< 2^{20})$ ，表示你找到的最长美丽数组。

样例1

输入

2
1048575
1048573

输出

1
113514
2
1048573 1048575

说明

对于第二组测试数据，找到的最长美丽数组 $a$ 为 {$1048573,1048575$} 。检查发现， $1048573<2^{20}，1048575<2^{20}$ ，且 $1048573$ & $1048575=1048573$ 。可以证明，不存在长度大于 $2$ 的美丽数组。