数论

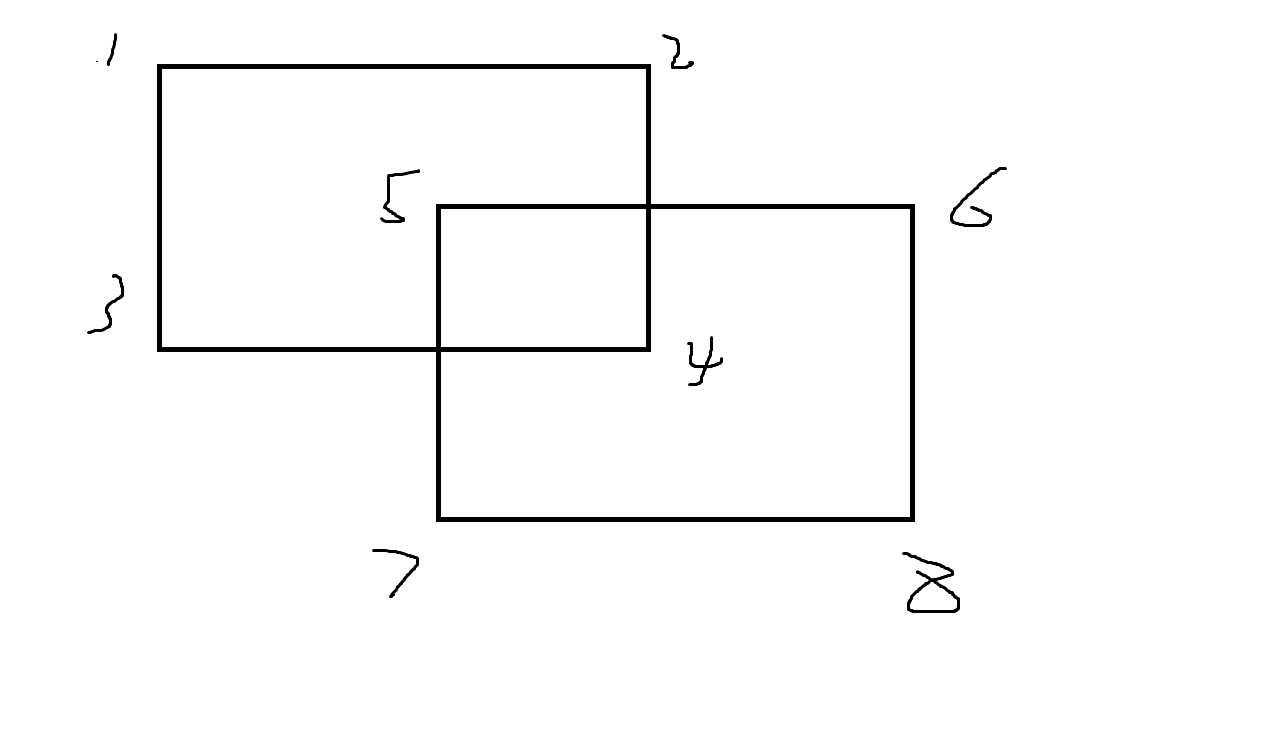对于两个矩形相交，相交矩形其实就是以长为min(4,8)的横坐标-max(3,7)的横坐标，宽为min(1,5)的横坐标-max(3,7)的纵坐标坐标。同理三矩形相交等于两个矩形的相交矩形与第三个矩形的相交矩形可以直接推3个矩形的，也可以通过前两个相交矩形与第三个.

代码如下

cpp

#include <bits/stdc++.h>
using namespace std;
#define N 100005
void solve(){
	int x1,y1,w1,h1;
	int x2,y2,w2,h2;
	int x3,y3,w3,h3;
	cin>>x1>>y1>>w1>>h1;
	cin>>x2>>y2>>w2>>h2;
	cin>>x3>>y3>>w3>>h3;
	int w=min({x1+w1,x2+w2,x3+w3})-max({x1,x2,x3});
	int h=min({y1,y2,y3})-max({y1-h1, y2-h2, y3-h3});
	if(w<=0||h<=0){
		cout<<0<<'\n';
	}
	else{
		cout<<w*h<<'\n';
	}
}
signed main() {
	ios::sync_with_stdio(0);
	cin.tie(0);
	solve();
	return 0;
}

python

def solve():
    import sys
    input = sys.stdin.read
    data = list(map(int, input().split()))
    
    # 读取三个矩形的参数
    x1, y1, w1, h1 = data[0:4]
    x2, y2, w2, h2 = data[4:8]
    x3, y3, w3, h3 = data[8:12]
    
    # 计算重叠的宽度
    overlap_w = min(x1 + w1, x2 + w2, x3 + w3) - max(x1, x2, x3)
    
    # 计算重叠的高度
    overlap_h = min(y1, y2, y3) - max(y1 - h1, y2 - h2, y3 - h3)
    
    # 判断是否有重叠
    if overlap_w <= 0 or overlap_h <= 0:
        print(0)
    else:
        print(overlap_w * overlap_h)

if __name__ == "__main__":
    solve()

java

import java.util.Scanner;

public class Main {
    public static void main(String[] args){
        Scanner sc = new Scanner(System.in);
        
        // 读取三个矩形的参数
        int x1 = sc.nextInt();
        int y1 = sc.nextInt();
        int w1 = sc.nextInt();
        int h1 = sc.nextInt();
        
        int x2 = sc.nextInt();
        int y2 = sc.nextInt();
        int w2 = sc.nextInt();
        int h2 = sc.nextInt();
        
        int x3 = sc.nextInt();
        int y3 = sc.nextInt();
        int w3 = sc.nextInt();
        int h3 = sc.nextInt();
        
        // 计算重叠的宽度
        int overlapW = Math.min(Math.min(x1 + w1, x2 + w2), x3 + w3) - Math.max(Math.max(x1, x2), x3);
        
        // 计算重叠的高度
        int overlapH = Math.min(Math.min(y1, y2), y3) - Math.max(Math.max(y1 - h1, y2 - h2), y3 - h3);
        
        // 判断是否有重叠
        if(overlapW <= 0 || overlapH <= 0){
            System.out.println(0);
        }
        else{
            System.out.println((long)overlapW * overlapH);
        }
        
        sc.close();
    }
}

题目描述

给出$3$组点坐标$(x, y, w, h)，-1000<x,y<1000，w,h$为正整数。

$(x, y, w, h)$表示平面直角坐标系中的一个矩形：

$x, y$为矩形左上角坐标点，$w, h$向右$w$，向下$h$。

$(x, y, w, h)$表示$x$轴$(x, x+w)$和$y$轴$(y, y-h)$围成的矩形区域；

$(0, 0, 2, 2)$表示$x$轴$(0, 2)$和$y$轴$(0, -2)$围成的矩形区域；

$(3, 5, 4, 6)$表示$x$轴$(3, 7)$和$y$轴$(5, -1)$围成的矩形区域；

求$3$组坐标构成的矩形区域重合部分的面积。

输入描述

$3$行输入分别为$3$个矩形的位置，分别代表“左上角$x$坐标”，“左上角y坐标”，“矩形宽”，“矩形高” $-1000 ≤ x,y < 1000$

输出描述

输出$3$个矩形相交的面积，不相交的输出$0$。

样例1

输入

1 6 4 4
3 5 3 4
0 3 7 3

输出

2

说明