解题思路

核心结论（贪心 + 交换论证） 设多重集的整体 MEX 为 m，即 m 是最小的使得 m 不在数组中的非负整数。要使前缀 MEX 总和最大，前 m 个位置必须依次放入 0,1,2,…,m-1，之后的元素任意。 理由：前缀第 i 次把 MEX 从 i-1 提升到 i 的唯一方式，是在此前缀里第一次补齐缺少的数 i-1。若把任何一个“首次出现的 k（k<m）”放晚了，则在它被放到位之前的所有位置，MEX 都无法达到本可达到的更大值，前缀总和严格变小。以交换为证：若在前 m 个位置存在一个不是目标的数，把它与之后最近的所需数交换不会变差，反复进行得到唯一最优前缀顺序 0,1,…,m-1。

由此，最大前缀 MEX 和可直接写成

题目内容

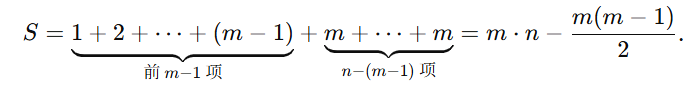
包包有一个长度为 $n$ 的数组 $a$ 。你可以将 $a$ 任意重排，得到一个新的数组，我们称之为 $a'$。定义一个长度为 $n$ 的数组 $b$，其中 $b_i= MEX(a’_ 1,a’_ 2,…,a’_ i)$。你需要最大化数组中的元素之和。

你需要输出最大的元素和，以及有多少种可能的重排 $a$，使得 $b$ 中的元素和最大化。由于重排方案数可能很大，你只需要输出其对 $998244353$ 取模后的结果。

【名词解释】

$MEX$：整数数组的 $MEX$ 定义为没有出现在数组中的最小非负整数。例如 $MEX${$1,2,3$}$=0、MEX${$0,2,5$}$= 1$ 。

输入描述

第一行输入一个整数 $n(1 ≤n ≤ 2·10^5)$ ，表示数组 $a$ 的长度。

第二行输入 $n$ 个整数 $a_1,a_2,···,a_n(0 ≤ ai ≤ 10^9)$，表示数组 $a$ 的元素。

输出描述

一行输出两个整数，表示 $b$ 的元素和以及 $a$ 的重排数量对 $998244353$ 取模后的结果。

样例1

输入

3
1 0 1

输出

5 1

说明

将 $a$ 重排为 {$0,1,1$} 后，数组 $b$ 为 {$1,2,2$}，元素和为 $5$ 。可以证明不存在一个重排使得数组 $b$ 的元素和大于 $5$ ，且仅有这一种重排方案满足条件。