思路与做法

• 索引消模：用 $s2=s+s$，则 $A_{r,c}=s2[(n-r)+c]$，避免每格做取模。

• 最大矩形（全 $0$）：维护直方图高度 $H[c]$（当前行该列为 $0$ 则 $H[c]\leftarrow H[c]+1$，否则 $H[c]\leftarrow 0$），对每一行用单调栈在 $O(n)$ 求“柱状图最大矩形”，总 $O(n^2)$。

• 最大直角等腰三角形（全 $0$）：两向 $DP$，自底向上、滚动一行，空间 $O(n)$、时间 $O(n^2)$。

  • 向右下（顶点在左上）：

  

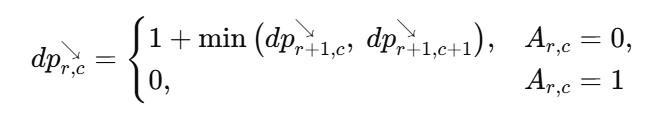
  • 向左下（顶点在右上）：

  

  • 每得高 $h$，面积为 $h(h+1)/2$，实时更新最大值。

• 答案：矩形最大面积与两向三角形最大面积取最大。

• 复杂度：时间 $O(n^2)$，空间 $O(n)$。

C++

#include <bits/stdc++.h>
using namespace std;

// 手写数组栈，常数更小
static int st_arr[5005];

// 单行直方图最大矩形
inline int maxRect(vector<int>& h) {
    int n = (int)h.size(), top = -1, ans = 0;
    for (int i = 0; i <= n; ++i) {
        int cur = (i == n ? 0 : h[i]);
        while (top >= 0 && h[st_arr[top]] > cur) {
            int height = h[st_arr[top--]];
            int left = (top >= 0 ? st_arr[top] : -1);
            int width = i - left - 1;
            int area = height * width;
            if (area > ans) ans = area;
        }
        st_arr[++top] = i;
    }
    return ans;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    string s;
    if (!(cin >> s)) return 0;
    int n = (int)s.size();
    string s2 = s + s; // A_{r,c} = s2[(n - r) + c]

    // 1) 最大矩形
    vector<int> height(n, 0);
    int bestRect = 0;
    for (int r = 0; r < n; ++r) {
        int base = n - r;
        const char* rowp = s2.data() + base;
        for (int c = 0; c < n; ++c) {
            if (rowp[c] == '0') height[c] += 1;
            else height[c] = 0;
        }
        int val = maxRect(height);
        if (val > bestRect) bestRect = val;
    }

    // 2) 最大三角形（两向 DP）
    long long bestTri = 0;
    vector<int> nextDR(n, 0), curDR(n, 0);
    vector<int> nextDL(n, 0), curDL(n, 0);

    for (int r = n - 1; r >= 0; --r) {
        int base = n - r;
        const char* rowp = s2.data() + base;
        for (int c = 0; c < n; ++c) {
            if (rowp[c] == '0') {
                int v1 = nextDR[c];
                int v2 = (c + 1 < n ? nextDR[c + 1] : 0);
                int h1 = 1 + (v1 < v2 ? v1 : v2);
                curDR[c] = h1;
                long long a1 = 1LL * h1 * (h1 + 1) / 2;
                if (a1 > bestTri) bestTri = a1;

                int w1 = nextDL[c];
                int w2 = (c - 1 >= 0 ? nextDL[c - 1] : 0);
                int h2 = 1 + (w1 < w2 ? w1 : w2);
                curDL[c] = h2;
                long long a2 = 1LL * h2 * (h2 + 1) / 2;
                if (a2 > bestTri) bestTri = a2;
            } else {
                curDR[c] = 0;
                curDL[c] = 0;
            }
        }
        nextDR.swap(curDR);
        nextDL.swap(curDL);
    }

    long long ans = max<long long>(bestRect, bestTri);
    cout << ans << '\n';
    return 0;
}

Python

import sys

def max_rect(h):
    # 单调栈求直方图最大矩形
    st = []
    ans = 0
    n = len(h)
    for i in range(n + 1):
        cur = 0 if i == n else h[i]
        while st and h[st[-1]] > cur:
            height = h[st.pop()]
            left = -1 if not st else st[-1]
            width = i - left - 1
            area = height * width
            if area > ans:
                ans = area
        st.append(i)
    return ans

def solve():
    s = sys.stdin.readline().strip()
    n = len(s)
    s2 = s + s  # A[r][c] = s2[(n - r) + c]

    # 1) 最大矩形
    height = [0] * n
    best_rect = 0
    for r in range(n):
        base = n - r
        row = s2[base:base + n]
        for c in range(n):
            if row[c] == '0':
                height[c] += 1
            else:
                height[c] = 0
        val = max_rect(height)
        if val > best_rect:
            best_rect = val

    # 2) 最大三角形（两向 DP）
    best_tri = 0
    nextDR = [0] * n
    nextDL = [0] * n
    curDR  = [0] * n
    curDL  = [0] * n

    for r in range(n - 1, -1, -1):
        base = n - r
        row = s2[base:base + n]
        for c in range(n):
            if row[c] == '0':
                v1 = nextDR[c]
                v2 = nextDR[c + 1] if c + 1 < n else 0
                h1 = 1 + (v1 if v1 < v2 else v2)
                curDR[c] = h1
                a1 = h1 * (h1 + 1) // 2
                if a1 > best_tri:
                    best_tri = a1

                w1 = nextDL[c]
                w2 = nextDL[c - 1] if c - 1 >= 0 else 0
                h2 = 1 + (w1 if w1 < w2 else w2)
                curDL[c] = h2
                a2 = h2 * (h2 + 1) // 2
                if a2 > best_tri:
                    best_tri = a2
            else:
                curDR[c] = 0
                curDL[c] = 0

        nextDR, curDR = curDR, nextDR
        nextDL, curDL = curDL, nextDL

    print(max(best_rect, best_tri))

if __name__ == "__main__":
    solve()

Java

import java.io.*;
import java.util.*;

public class Main {
    static int maxRect(int[] h) {
        int n = h.length;
        Deque<Integer> st = new ArrayDeque<>();
        int ans = 0;
        for (int i = 0; i <= n; i++) {
            int cur = (i == n ? 0 : h[i]);
            while (!st.isEmpty() && h[st.peek()] > cur) {
                int height = h[st.pop()];
                int left = st.isEmpty() ? -1 : st.peek();
                int width = i - left - 1;
                int area = height * width;
                if (area > ans) ans = area;
            }
            st.push(i);
        }
        return ans;
    }

    public static void main(String[] args) throws Exception {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        String s = br.readLine().trim();
        int n = s.length();
        String s2 = s + s; // A[r][c] = s2[(n - r) + c]

        // 1) 最大矩形
        int[] height = new int[n];
        int bestRect = 0;
        for (int r = 0; r < n; r++) {
            int base = n - r;
            // 直接按字符访问
            for (int c = 0; c < n; c++) {
                char ch = s2.charAt(base + c);
                if (ch == '0') height[c]++;
                else height[c] = 0;
            }
            bestRect = Math.max(bestRect, maxRect(height));
        }

        // 2) 最大三角形（两向 DP）
        long bestTri = 0;
        int[] nextDR = new int[n], curDR = new int[n];
        int[] nextDL = new int[n], curDL = new int[n];

        for (int r = n - 1; r >= 0; r--) {
            int base = n - r;
            for (int c = 0; c < n; c++) {
                char ch = s2.charAt(base + c);
                if (ch == '0') {
                    int v1 = nextDR[c];
                    int v2 = (c + 1 < n ? nextDR[c + 1] : 0);
                    int h1 = 1 + Math.min(v1, v2);
                    curDR[c] = h1;
                    long a1 = 1L * h1 * (h1 + 1) / 2;
                    if (a1 > bestTri) bestTri = a1;

                    int w1 = nextDL[c];
                    int w2 = (c - 1 >= 0 ? nextDL[c - 1] : 0);
                    int h2 = 1 + Math.min(w1, w2);
                    curDL[c] = h2;
                    long a2 = 1L * h2 * (h2 + 1) / 2;
                    if (a2 > bestTri) bestTri = a2;
                } else {
                    curDR[c] = 0;
                    curDL[c] = 0;
                }
            }
            int[] tmp;
            tmp = nextDR; nextDR = curDR; curDR = tmp;
            tmp = nextDL; nextDL = curDL; curDL = tmp;
        }

        long ans = Math.max(bestRect, bestTri);
        System.out.println(ans);
    }
}

题目内容

给定一个长度为$n$的二进制字符串$s$，由$0$和$1$字符组成。我们需要构建一个行数为$n$，列数为$n$的方表，由$0$和$1$字符组成。第一行为原始字符串 $s$，第二行为字符串$s$向右循环移动一个，第三行为字符串$s$向右循环移动两个，以此类推。

求表中所有由$0$组成的三角形或矩形的最大面积值。

第一行是字符串$s$。

第二行是字符串$s$向右循环移动一个位置。

第$i$行是字符串$s$向右循环移动$i-1$个位置。

输入描述

输入一个长度为$n$的二进制字符串$s$，仅包含$0$和$1$字符，其中$1≤n≤5000$

输出描述

在一行上输出$n$个整数，代表对于每一个$i$的答案。

样例1

输入

00110			

输出

6

说明

在构造的方表中，最大由$0$组成的三角形面积为$6$，构造的表格如下:

$00110$

$00011$

$10001$

$11000$

$01100$