思路

先看两种情况的贡献: 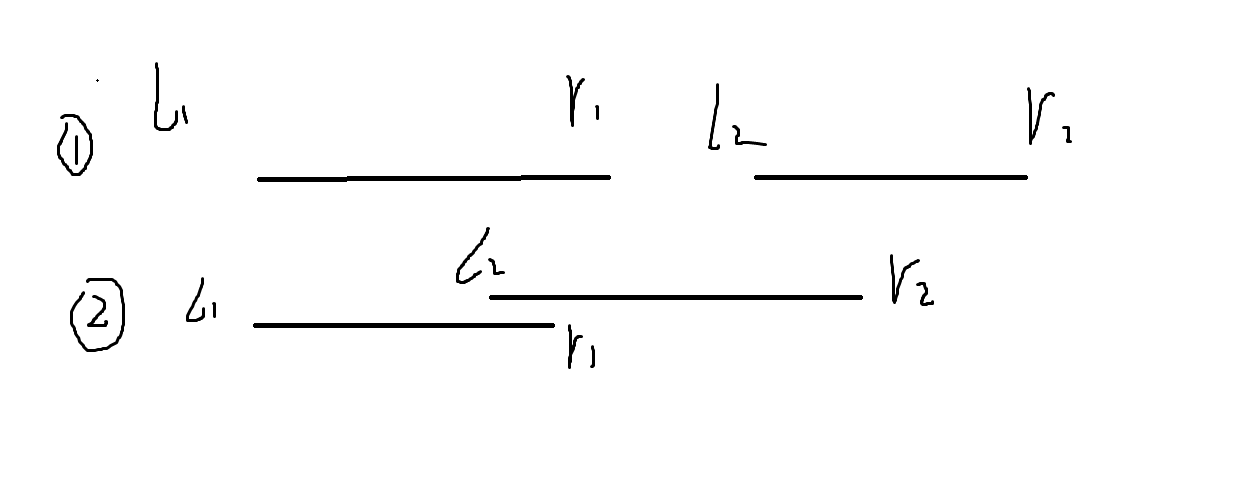1.第一种的贡献也就是l1到r1的总和加上l2到r2的总和.$\\$ 2.第二种的贡献是l1到r1的总和加上l2到r2的总和再加上l2到r1的总和

代码如下

cpp

#include <bits/stdc++.h>
using namespace std;

#define N 200005
#define int long long

int pre[N];
int n, q;
int l1, r1, l2, r2;
int sum = 0;

// 函数：计算区间和
int get_sum(int l, int r){
    if(l > r) return 0;
    return pre[r] - pre[l-1];
}

signed main() {
    // 优化输入输出速度
    ios::sync_with_stdio(false);
    cin.tie(NULL);
    
    cin >> n >> q;
    for(int i = 1; i <= n; i++){
        int x;
        cin >> x;
        pre[i] = pre[i-1] + x;
        sum += x;
    }
    
    while(q--){
        cin >> l1 >> r1 >> l2 >> r2;
        
        // 计算两个区间的和
        int sum1 = get_sum(l1, r1);
        int sum2 = get_sum(l2, r2);
        
        // 计算重叠区间的和
        int overlap_l = max(l1, l2);
        int overlap_r = min(r1, r2);
        int sum_overlap = get_sum(overlap_l, overlap_r);
        
        // 根据是否有重叠计算结果
        int res = sum;
        if(overlap_l <= overlap_r){
            // 有重叠
            res += sum1 + sum2 + sum_overlap;
        }
        else{
            // 无重叠
            res += sum1 + sum2;
        }
        
        cout << res << '\n';
    }
    
    return 0;
}

python

import sys
import threading

def main():
    import sys

    def input():
        return sys.stdin.readline()

    n, q = map(int, sys.stdin.readline().split())
    a = list(map(int, sys.stdin.readline().split()))
    
    prefix_sum = [0] * (n + 1)
    for i in range(1, n+1):
        prefix_sum[i] = prefix_sum[i-1] + a[i-1]
    
    initial_sum = prefix_sum[n]
    
    for _ in range(q):
        l1, r1, l2, r2 = map(int, sys.stdin.readline().split())
        
        # 计算两个区间的和
        sum1 = prefix_sum[r1] - prefix_sum[l1 - 1]
        sum2 = prefix_sum[r2] - prefix_sum[l2 - 1]
        
        # 计算重叠区间的和
        overlap_l = max(l1, l2)
        overlap_r = min(r1, r2)
        if overlap_l <= overlap_r:
            sum_overlap = prefix_sum[overlap_r] - prefix_sum[overlap_l - 1]
        else:
            sum_overlap = 0
        
        # 计算操作后的总和
        # sum1 和 sum2 中，重叠部分被计算了两次，需要再加上重叠部分
        total = initial_sum + sum1 + sum2 + sum_overlap
        print(total)

# 使用 threading 来加快输入速度，避免超时
threading.Thread(target=main).start()

java

import java.io.*;
import java.util.*;

public class Main {
    public static void main(String[] args) throws IOException {
        // 使用 BufferedReader 和 BufferedWriter 进行高效输入输出
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
        StringTokenizer st = new StringTokenizer(br.readLine());
        
        int n = Integer.parseInt(st.nextToken());
        int q = Integer.parseInt(st.nextToken());
        
        long[] a = new long[n];
        st = new StringTokenizer(br.readLine());
        for(int i = 0; i < n; i++) {
            a[i] = Long.parseLong(st.nextToken());
        }
        
        // 计算前缀和
        long[] prefix_sum = new long[n + 1];
        for(int i = 1; i <= n; i++) {
            prefix_sum[i] = prefix_sum[i-1] + a[i-1];
        }
        
        long initial_sum = prefix_sum[n];
        
        for(int i = 0; i < q; i++) {
            st = new StringTokenizer(br.readLine());
            int l1 = Integer.parseInt(st.nextToken());
            int r1 = Integer.parseInt(st.nextToken());
            int l2 = Integer.parseInt(st.nextToken());
            int r2 = Integer.parseInt(st.nextToken());
            
            // 计算两个区间的和
            long sum1 = prefix_sum[r1] - prefix_sum[l1 - 1];
            long sum2 = prefix_sum[r2] - prefix_sum[l2 - 1];
            
            // 计算重叠区间的和
            int overlap_l = Math.max(l1, l2);
            int overlap_r = Math.min(r1, r2);
            long sum_overlap = 0;
            if(overlap_l <= overlap_r){
                sum_overlap = prefix_sum[overlap_r] - prefix_sum[overlap_l -1];
            }
            
            // 计算操作后的总和
            long total = initial_sum + sum1 + sum2 + sum_overlap;
            bw.write(total + "\n");
        }
        
        // 刷新输出
        bw.flush();
        bw.close();
        br.close();
    }
}

题目内容

给出一个长度为$n$的整数数组$a$，下标从$1$开始。

$q$次询问，每次询问给出两个区间 $[l_1,r_1],[l_2,r_2]$，先让下标在$[l_1,r_1]$里的元素乘以$2$，再让下标在$[l_2,r_2]$里的元素乘以 $2$，输出每次询问操作后数组总和是多少?

询问是相互独立的，每次询问后都把数组还原为初始状态。

输入描述

第一行包含两个整数$n$ $q(1≤n,q≤2×10^5)$，表示数组大小和询问个数。

第二行包含 $n$ 个整数 $a_i(-10^5 ≤ a_i≤ 10^5)$，表示数组 $a$。

接下来$q$行，每行四个整数$l_1$ $r_1$ $l_2$ $r_2$ $(1 ≤ l_1 ≤ r_1 ≤ n , 1 ≤ l_2 ≤ r_2 ≤ n)$，表示操作区间。

输出描述

输出包含$q$行，每行一个整数，表示每次询问操作后的数组总和。

样例1

输入

3 2
1 2 1
1 2 2 3
1 1 2 2

输出

12
7

说明

第一次询问:$[1,2]$ 内元素乘 $2$，$a=[2,4,1]$，$[2,3]$ 内元素乘 $2$，$a=「2,8,2]$，数组总和是 $12$。

第二次询问:$[1,1]$内元素乘 $2$，$a=[2,2,1]$，$[2,2]$内元素乘 $2$，$a=[2,4,1]$，数组总和是 $7$。