解题思路

• 将过程按“转一圈”为一个批次（轮）。

  • 若玩家数 m ≤ n：每一圈只能坐满前 m 个吊舱，且同一批玩家每圈固定坐吊舱 1..m。连续 L 圈后，第 p(1..m) 位玩家总幸福值为 L * h_p。答案就是前 m 个吊舱幸福值的最大者（并取最靠前下标）。

  • 若玩家数 m > n：每圈恰有 n 人上车，队列整体向后旋转 n 位。把所有上车时刻按时间线排成 T = n * L 次“座位事件”。第 j(0..T-1) 次事件使用的吊舱是 (j mod n) + 1，被安排的玩家是“队列中的第 j 位”（跨圈连续计数）。于是第 p 位玩家的上车时刻是所有 j ≡ p-1 (mod m) 且 0 ≤ j < T。

    • 因而第 p 位玩家上车次数

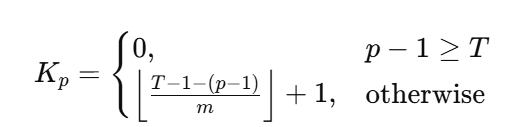
• 其每次对应的吊舱序号按模 n 的等差序列：idx_k = ((p-1) + k*m) mod n（0-based）。这是在 n 上以步长 m 的循环走访，周期为 len = n / gcd(n, m)，并被分成 g = gcd(n, m) 个不相交的循环。
  • 对每个循环（按访问顺序）预处理前缀和（再拼接一遍以便处理从任意起点取余数个元素）。则

其中 start 是该玩家首次上车对应的下标在该循环顺序中的位置。

• 计算所有 p=1..m 的总幸福值，取最大者；若并列取最小的 p。

所用算法：数论中的 gcd 与模循环分解、等差序列取模、前缀和（循环数组加倍法）。

复杂度分析

• 预处理将 n 个吊舱索引分解为 g = gcd(n,m) 个循环，总长度为 n，并为每个循环构造长度 2*len 的前缀和。总体时间与空间均为 O(n)。
• 遍历所有玩家 p=1..m，每人 O(1) 计算其总幸福值，时间 O(m)，空间 O(1) 额外。
• 总体复杂度：时间 O(n + m)，空间 O(n)。数据范围下可行。
• 所有和乘均在 64 位整型范围内（因为单人最多乘到 L * max(h_i) ≤ 1e9 * 1e9 = 1e18）。

代码实现

Python

# -*- coding: utf-8 -*-
# 题意实现：给定 n, m, L 和 n 个吊舱幸福值 h_i，求多多应占的队伍位置（1..m），使得经过 L 圈的总幸福值最大；并列取最靠前。

import sys
from math import gcd

def solve(n, m, L, h):
    # 情况一：m ≤ n，固定每圈前 m 个吊舱被使用
    if m <= n:
        best_idx = 1
        best_val = h[0] * L  # Python int 无溢出
        for i in range(1, m):
            val = h[i] * L
            if val > best_val:
                best_val = val
                best_idx = i + 1
        return best_idx

    # 情况二：m > n，构造循环并用前缀和 O(1) 求和
    T = n * L  # 总上车事件数
    # 预分解 idx -> 所属循环 id 及在循环中的位置
    g = gcd(n, m)
    visited = [False] * n
    cid = [-1] * n           # 每个吊舱索引属于哪个循环
    pos = [-1] * n           # 在循环访问顺序中的位置
    cycles = []              # 每个循环中按访问顺序的幸福值列表
    cyc_sum = []             # 每个循环的总和
    pref = []                # 每个循环的双倍前缀和数组

    # 构造循环：从尚未访问的 i 出发，每次加 m 模 n
    for i in range(n):
        if not visited[i]:
            cur = i
            ids = []
            while not visited[cur]:
                visited[cur] = True
                ids.append(cur)
                cur = (cur + m) % n
            c_id = len(cycles)
            for j, idx in enumerate(ids):
                cid[idx] = c_id
                pos[idx] = j
            vals = [h[idx] for idx in ids]
            cycles.append(vals)
            cyc_sum.append(sum(vals))
            # 双倍前缀和，方便从任意起点取连续 r 段（环形）
            dbl = vals + vals
            ps = [0]
            for v in dbl:
                ps.append(ps[-1] + v)
            pref.append(ps)

    best_idx = 1
    best_val = -1

    for p in range(1, m + 1):
        # 该玩家上车次数 K_p
        if p - 1 >= T:
            k = 0
        else:
            k = ((T - 1) - (p - 1)) // m + 1

        if k == 0:
            total = 0
        else:
            # 首次出现的全局事件 j0 = p-1，对应的吊舱下标 idx0 = (p-1) % n
            idx0 = (p - 1) % n
            c = cid[idx0]
            s = pos[idx0]
            length = len(cycles[c])
            q, r = divmod(k, length)
            total = q * cyc_sum[c]
            if r > 0:
                ps = pref[c]
                total += ps[s + r] - ps[s]

        if total > best_val:
            best_val = total
            best_idx = p

    return best_idx


def main():
    data = sys.stdin.read().strip().split()
    n, m, L = map(int, data[:3])
    h = list(map(int, data[3:3 + n]))
    print(solve(n, m, L, h))

if __name__ == "__main__":
    main()

Java

// 题意实现（ACM 风格）：读取输入，输出最佳位置。使用 long 存储和乘积，避免溢出。
import java.io.*;
import java.util.*;

public class Main {
    static int n, m;
    static long L;
    static long[] h;

    // 求解函数
    static int solve() {
        if (m <= n) {
            // 前 m 个吊舱固定被使用
            int bestIdx = 1;
            long bestVal = h[0] * L;
            for (int i = 1; i < m; i++) {
                long val = h[i] * L;
                if (val > bestVal) {
                    bestVal = val;
                    bestIdx = i + 1;
                }
            }
            return bestIdx;
        }

        long T = (long) n * L; // 总上车事件数
        int g = gcd(n, m);

        boolean[] visited = new boolean[n];
        int[] cid = new int[n];      // 每个索引所属循环 id
        int[] pos = new int[n];      // 在循环序中的位置
        Arrays.fill(cid, -1);
        Arrays.fill(pos, -1);

        ArrayList<long[]> cycles = new ArrayList<>(); // 每个循环的值序列
        ArrayList<Long> cycSum = new ArrayList<>();   // 每个循环的总和
        ArrayList<long[]> pref = new ArrayList<>();   // 每个循环的双倍前缀和

        // 构造循环：i -> (i + m) % n
        for (int i = 0; i < n; i++) {
            if (!visited[i]) {
                ArrayList<Integer> ids = new ArrayList<>();
                int cur = i;
                while (!visited[cur]) {
                    visited[cur] = true;
                    ids.add(cur);
                    cur = (cur + m) % n;
                }
                int cId = cycles.size();
                int len = ids.size();
                long[] vals = new long[len];
                for (int j = 0; j < len; j++) {
                    int idx = ids.get(j);
                    cid[idx] = cId;
                    pos[idx] = j;
                    vals[j] = h[idx];
                }
                cycles.add(vals);
                long s = 0;
                for (long v : vals) s += v;
                cycSum.add(s);

                // 双倍前缀和
                long[] ps = new long[len * 2 + 1];
                ps[0] = 0;
                for (int j = 0; j < len * 2; j++) {
                    ps[j + 1] = ps[j] + vals[j % len];
                }
                pref.add(ps);
            }
        }

        int bestIdx = 1;
        long bestVal = -1;

        for (int p = 1; p <= m; p++) {
            long k;
            if (p - 1 >= T) k = 0;
            else k = ((T - 1) - (p - 1)) / m + 1;

            long total;
            if (k == 0) {
                total = 0;
            } else {
                int idx0 = (p - 1) % n;
                int c = cid[idx0];
                int s = pos[idx0];
                int len = cycles.get(c).length;
                long q = k / len;
                int r = (int) (k % len);
                total = q * cycSum.get(c);
                if (r > 0) {
                    long[] ps = pref.get(c);
                    total += ps[s + r] - ps[s];
                }
            }

            if (total > bestVal) {
                bestVal = total;
                bestIdx = p;
            }
        }

        return bestIdx;
    }

    static int gcd(int a, int b) {
        while (b != 0) {
            int t = a % b;
            a = b;
            b = t;
        }
        return a;
    }

    public static void main(String[] args) throws Exception {
        // 读入：第一行 n m L；第二行 n 个 h_i
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine().trim());
        n = Integer.parseInt(st.nextToken());
        m = Integer.parseInt(st.nextToken());
        L = Long.parseLong(st.nextToken());
        h = new long[n];
        st = new StringTokenizer(br.readLine().trim());
        for (int i = 0; i < n; i++) {
            h[i] = Long.parseLong(st.nextToken());
        }
        System.out.println(solve());
    }
}

C++

// 题意实现（ACM 风格）：C++17，long long 处理乘加。含中文注释。
#include <bits/stdc++.h>
using namespace std;

static long long n_, m_, L_;
static vector<long long> h;

long long gcd_ll(long long a, long long b) {
    while (b) { long long t = a % b; a = b; b = t; }
    return a;
}

int solve() {
    long long n = n_, m = m_, L = L_;

    if (m <= n) {
        // 每圈只会用到前 m 个吊舱
        int bestIdx = 1;
        long long bestVal = h[0] * L;
        for (int i = 1; i < (int)m; ++i) {
            long long val = h[i] * L;
            if (val > bestVal) {
                bestVal = val;
                bestIdx = i + 1;
            }
        }
        return bestIdx;
    }

    long long T = n * L; // 总上车事件数
    long long g = gcd_ll(n, m);

    vector<int> visited(n, 0), cid(n, -1), pos(n, -1);
    vector<vector<long long>> cycles;   // 各循环的值序列
    vector<long long> cycSum;           // 各循环总和
    vector<vector<long long>> pref;     // 各循环双倍前缀和

    // 构造循环：i -> (i + m) % n
    for (int i = 0; i < (int)n; ++i) {
        if (!visited[i]) {
            vector<int> ids;
            int cur = i;
            while (!visited[cur]) {
                visited[cur] = 1;
                ids.push_back(cur);
                cur = (cur + (int)m) % (int)n;
            }
            int cId = (int)cycles.size();
            int len = (int)ids.size();
            vector<long long> vals(len);
            for (int j = 0; j < len; ++j) {
                int idx = ids[j];
                cid[idx] = cId;
                pos[idx] = j;
                vals[j] = h[idx];
            }
            cycles.push_back(vals);
            long long s = 0;
            for (auto v : vals) s += v;
            cycSum.push_back(s);

            vector<long long> ps(2 * len + 1, 0);
            for (int j = 0; j < 2 * len; ++j) {
                ps[j + 1] = ps[j] + vals[j % len];
            }
            pref.push_back(ps);
        }
    }

    int bestIdx = 1;
    long long bestVal = -1;

    for (int p = 1; p <= (int)m; ++p) {
        long long k;
        if ((long long)(p - 1) >= T) k = 0;
        else k = ((T - 1) - (p - 1)) / m + 1;

        long long total = 0;
        if (k > 0) {
            int idx0 = (p - 1) % (int)n;
            int c = cid[idx0];
            int s = pos[idx0];
            int len = (int)cycles[c].size();
            long long q = k / len;
            int r = (int)(k % len);
            total = q * cycSum[c];
            if (r > 0) {
                const auto &ps = pref[c];
                total += ps[s + r] - ps[s];
            }
        }

        if (total > bestVal) {
            bestVal = total;
            bestIdx = p;
        }
    }

    return bestIdx;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cin >> n_ >> m_ >> L_;
    h.resize(n_);
    for (int i = 0; i < n_; ++i) cin >> h[i];
    cout << solve() << "\n";
    return 0;
}

题目内容

多多来到游乐场坐摩天轮，摩天轮共有 $n$ 个吊舱，包括多多在内总共即将有 $m$ 名玩家排队，每个吊舱最多只能坐一名玩家，每名玩家游玩结束后会到队尾继续排队。每当有一名玩家离开吊舱，下一名排在队首的玩家会立即坐上这个空吊舱，在游玩过程中不会有玩家加入也不会有玩家离开。

第 $i$ 个吊舱的幸福指数为 $h_i$ ，坐到该吊舱的人会获得 $h_i$ 点幸福指数，多多提前掌握了现场的排队人数以及每个吊舱的幸福指数，他想在摩天轮转 $L$ 圈后获得最高的总幸福指数，问他需要抢到队伍中的第几个位置?如果多个位置的总幸福指数一样，多多想排到尽可能靠前的位置。

输入描述

第一行为三个正整数 $n,m,L(1≤n,m≤10^5,1≤L≤10^9)$

第二行为 $n$ 个整数 $h_1,h_2,...,hn (1≤h_i≤10^9)$

输出描述

输出队伍中幸福指款最高的位置，若存在多个位置满足条件，输出最靠前的那个位置。

补充说明

对于 $60$%的数据 , $1≤n,m,L≤1000$

对于 $100$%的数据，$1≤n,m≤10^5,1≤L≤10^9,1≤h_i≤10^9$

样例1

输入

5 3 1000000000
1 2 3 4 5

输出

3

说明

$5$ 个吊舱 $3$ 名玩家，每一轮都只能坐满前 $3$ 个吊舱的位置，且 $3$ 个位置的幸福指数总是 $1,2,3$ ，经过 $10^9$ 轮后，玩家的幸福指教分别为 $1 ×10^9,2 × 10^9,3× 10^9$ ，最终第 $3$ 个位置的幸福指数最高。

样例2

输入

3 6 2
2 3 1

输出

2

说明

$3$ 个吊舱 $6$ 名玩家，第一轮玩家 $1,2,3$ 坐上摩天轮，分别获得幸福指数 $2,3,1$，第二轮玩家 $4,5,6$ 坐上摩天轮，分别获得幸福指数 $2,3,1$，$2$ 轮过后第 $2$ 名与第 $5$ 名玩家都获得 $3$ 点幸福指数，取最小序号的位置 $2$ 输出答案。