#P3399. 第2题-小红的“葫芦”
-
1000ms
Tried: 120
Accepted: 35
Difficulty: 6
所属公司 :
字节
时间 :2025年8月17日
-
算法标签>组合计数
第2题-小红的“葫芦”
思路
-
频次统计:设不同取值共有 m 种,第 i 种值的出现次数为 ni。
-
组合计数:选择两种不同的值 i=j,从其中一种取 3 个,另一种取 2 个。对固定的 (i,j),可行子序列数为 (3ni)(2nj)。对所有有序对求和,答案为
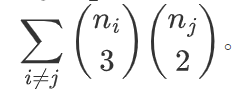
-
化简到线性:令 S2=∑i(2ni),S3=∑i(3ni)。则

-
实现:统计频次并一次遍历计算 S2、S3 与自项 ∑i(3ni)(2ni),最终答案为 S3S2−∑i(3ni)(2ni)。
-
正确性:对子序列而言,只需选择位置,不受交错顺序影响;因此对每对取值分别独立选择 3 与 2 个位置并合并即得唯一子序列。
C++
#include <bits/stdc++.h>
using namespace std;
// 计算 c 取 2 和 取 3 的组合数,c < k 时返回 0
static inline unsigned long long C2(unsigned long long c) {
return (c >= 2) ? (c * (c - 1) / 2) : 0ULL;
}
static inline unsigned long long C3(unsigned long long c) {
return (c >= 3) ? (c * (c - 1) * (c - 2) / 6) : 0ULL;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int n;
if (!(cin >> n)) return 0;
unordered_map<long long, int> freq;
freq.reserve(n * 2);
for (int i = 0; i < n; ++i) {
long long x;
cin >> x;
++freq[x];
}
// 统计所有种类的频次
vector<unsigned long long> counts;
counts.reserve(freq.size());
for (auto &kv : freq) counts.push_back((unsigned long long)kv.second);
// 计算 S2, S3 及自项之和
unsigned long long S2 = 0, S3 = 0;
unsigned long long selfSum = 0; // sum C(ni,3) * C(ni,2)
for (auto c : counts) {
unsigned long long c2 = C2(c);
unsigned long long c3 = C3(c);
S2 += c2;
S3 += c3;
// 使用 128 位避免中间乘法溢出
__int128 tmp = (__int128)c2 * (__int128)c3;
selfSum += (unsigned long long)tmp;
}
// 答案 = S3 * S2 - 自项之和
__int128 ans128 = (__int128)S3 * (__int128)S2 - (__int128)selfSum;
unsigned long long ans = (unsigned long long)ans128;
cout << ans << '\n';
return 0;
}
import sys
from collections import Counter
def C2(c: int) -> int:
return c * (c - 1) // 2 if c >= 2 else 0
def C3(c: int) -> int:
return c * (c - 1) * (c - 2) // 6 if c >= 3 else 0
def main():
data = sys.stdin.read().strip().split()
if not data:
return
it = iter(data)
n = int(next(it))
arr = [int(next(it)) for _ in range(n)]
cnt = Counter(arr)
S2 = 0
S3 = 0
self_sum = 0
for c in cnt.values():
c2 = C2(c)
c3 = C3(c)
S2 += c2
S3 += c3
self_sum += c2 * c3
ans = S3 * S2 - self_sum
print(ans)
if __name__ == "__main__":
main()
import java.io.*;
import java.util.*;
public class Main {
static long C2(long c) {
return c >= 2 ? c * (c - 1) / 2 : 0L;
}
static long C3(long c) {
return c >= 3 ? c * (c - 1) * (c - 2) / 6 : 0L;
}
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st;
String s = br.readLine();
if (s == null || s.isEmpty()) return;
int n = Integer.parseInt(s.trim());
List<Integer> vals = new ArrayList<>(n);
while (vals.size() < n) {
String line = br.readLine();
if (line == null) break;
st = new StringTokenizer(line);
while (st.hasMoreTokens() && vals.size() < n) {
vals.add(Integer.parseInt(st.nextToken()));
}
}
HashMap<Integer, Integer> freq = new HashMap<>(n * 2);
for (int x : vals) freq.put(x, freq.getOrDefault(x, 0) + 1);
long S2 = 0, S3 = 0, selfSum = 0;
for (int cInt : freq.values()) {
long c = cInt;
long c2 = C2(c);
long c3 = C3(c);
S2 += c2;
S3 += c3;
selfSum += c2 * c3;
}
long ans = S3 * S2 - selfSum;
System.out.println(ans);
}
}
题目内容
小红定义一个长度为 5 的数组是"葫芦”,当且仅当数组仅包含两种元素,其中一种出现次数为 2 ,另一种出现次数为 3 。例如、{1,1,4,1,4} 是葫芦,而 {1,2,3,4,5}、{6,6,6,6,6} 均不是葫芦。
现在小红拿到了一个数组,她想知道有多少长度为 5 的 子序列 是“葫芦”?
子序列 为从原数组中删除任意个(可以为零、可以为全部)元素得到的新数组。
输入描述
第一行输入一个正整数 n(1≦n≦5000) ,代表数组的长度。
第二行输入 n 个正整数 a1,a2,...,an(1≦ai≦109) 代表数组的元素。
输出描述
输出一个整数,代表“葫芦”的数量。
样例1
输入
6
1 1 4 5 1 4
输出
1
样例2
输入
6
1 1 4 4 4 1
输出
6
