思路与证明

• 设最终选择的区间为 $[l,r]$。将区间内元素乘上 $k$ 后，整个数组的 $gcd$ 为

  

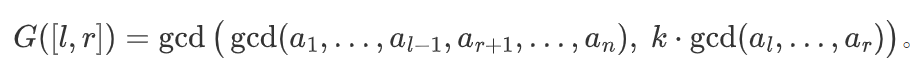
• 记 $H=\gcd(a_1,\dots,a_{l-1},a_{r+1},\dots,a_n)$、$I=\gcd(a_l,\dots,a_r)$、$g=\gcd(a_1,\dots,a_n)$，显然有 $\gcd(H,I)=g$。

• 将 $H=g\cdot h'$、$I=g\cdot i'$，且 $\gcd(h',i')=1$。则

  

• 因为 $\gcd(h',k)\le k$，故 $G([l,r])\le g\cdot k$。

• 当取整段 $[1,n]$ 时，$H=0$，于是 $G([1,n])=\gcd(0,k\cdot g)=k\cdot g$，达到上界。

• 结论：最大值恒为 $\boldsymbol{k\cdot \gcd(a_1,\dots,a_n)}$。

C++

#include <bits/stdc++.h>
using namespace std;

int main() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr);
	
	int T;
	if (!(cin >> T)) return 0;
	while (T--) {
		int n;
		long long k;
		cin >> n >> k;
		long long g = 0; // 维护全局gcd
		for (int i = 0; i < n; ++i) {
			long long x;
			cin >> x;
			g = std::gcd(g, x); // 逐步求gcd
		}
		// 答案为 k * gcd(a1..an)，范围可达1e18，long long可承受
		cout << g * k << "\n";
	}
	return 0;
}

Python

import sys
import math

def main():
	data = sys.stdin.read().strip().split()
	it = iter(data)
	T = int(next(it))
	out = []
	for _ in range(T):
		n = int(next(it))
		k = int(next(it))
		g = 0  # 全局gcd
		for _ in range(n):
			x = int(next(it))
			g = math.gcd(g, x)
		out.append(str(g * k))  # 结果为 k * gcd
	print("\n".join(out))

if __name__ == "__main__":
	main()

Java

import java.io.*;
import java.util.*;

public class Main {
	// 欧几里得算法求gcd
	static long gcd(long a, long b) {
		while (b != 0) {
			long t = a % b;
			a = b;
			b = t;
		}
		return Math.abs(a);
	}

	public static void main(String[] args) throws Exception {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		StringBuilder sb = new StringBuilder();
		int T = Integer.parseInt(br.readLine().trim());
		while (T-- > 0) {
			StringTokenizer st = new StringTokenizer(br.readLine());
			int n = Integer.parseInt(st.nextToken());
			long k = Long.parseLong(st.nextToken());
			st = new StringTokenizer(br.readLine());
			long g = 0; // 全局gcd
			for (int i = 0; i < n; i++) {
				long x = Long.parseLong(st.nextToken());
				g = gcd(g, x);
			}
			// 结果为 k * gcd(a1..an)
			sb.append(g * k).append('\n');
		}
		System.out.print(sb.toString());
	}
}

题目内容

小苯有一个长度为 $n$ 的数组 {$a_1,a_2,...,a_n$} ，他最多可以执行一次以下操作:

• 选择一个区间 $[l,r](1 ≦l≦r≦ n)$，将区间中所有数字都乘上 $k$ 。

他想知道，操作结束后，数组的 $gcd$ 最大可以变为多少，请你帮他算一算吧。

$gcd$，即最大公约数。例如，$12$ 和 $30$ 的公约数有 $1,2,3,6$ 其中最大的约数是 $6$ ，因此 $gcd(12,30)= 6$ 。

输入描述

每个测试文件包含多组测试数据。第一行输入一个整数 $T(1≦T≦100)$ 代表数据组数，每组测试数据描述如下

第一行输入两个正整数

$n,k(1≦n≦2×10^5;1≦k≦10^9)$ 代表数组中的元素个数、乘数。

第二行输入 $n$ 个整数 $a_1,a_2,...,a_n(0≦a_i≦10^9)$ ，表示数组 $a$ 。

除此之外，保证单个测试文件的 $n$ 之和不超过 $3×10^5$ 。

输出描述

对于每一组测试数据，新起一行，输出一个整数，表示操作结束后，数组的 $gcd$ 最大可以变为多少。

样例1

输入

2
5 3
1 1 3 6 9
3 1
1 2 3

输出

3
1

说明

对于第一组对试数据，可以选择 $[1,2]$ 这个区间执行操作，执行后数组变为 {$3,3,3,6,9$} ，此时数组的 $gcd$ 为 $3$ ，达到最大。

对于第二组测试数据，无论选择哪个区间执行操作，数组的 $gcd$ 都不会改变。