本题直接看很难看出规律，打表可以发现当$n$为偶数时规律很明显,如下图:

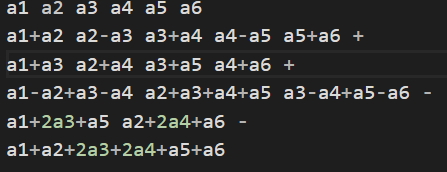
不难看出最后每个$a_i$的系数跟杨辉三角有关,手玩几个样例可以发现当$n$为$4$的倍数时最后一列是相减,非$4$的倍数时最后一列是相加,当$n$为奇数时可以先算一列转换成偶数来做.

记组合数$c(n,m)$,那么当n为偶数时最后一列的系数每两个数一组依次为$c(n/2-1,i/2)$,直接预处理组合数再根据上述规律算即可

c++

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e5+10,mod=1e9+7;
ll a[N],f[N],g[N];
int n;
ll qmi(ll a,ll b)
{
    ll res=1;
    while(b)
    {
        if(b&1)res=res*a%mod;
        b>>=1;
        a=a*a%mod;
    }
    return res;
}
void init()//预处理
{
    g[0]=f[0]=1;
    for(int i=1;i<N;i++)
    {
        f[i]=f[i-1]*i%mod;
        g[i]=g[i-1]*qmi(i,mod-2)%mod;
    }
}
ll c(ll n,ll m)
{
    if(n<m)return 0;
    return f[n]*g[n-m]%mod*g[m]%mod;
}
signed main()
{
    ios::sync_with_stdio(0);
    cin.tie(0),cout.tie(0);
    init();
    cin>>n;
    for(int i=1;i<=n;i++)cin>>a[i];
    if(n<=2)//特判n<=2的情况
    {
        cout<<(a[1]+a[2])%mod<<endl;
        return 0;
    }
    if(n&1)//n为奇数时可以转化成偶数来做
    {
        int mk=1;
        for(int i=1;i<n;i++)
        {
            a[i]=a[i]+a[i+1]*mk;
            mk=-mk;
        }
        n--;
    }
    int mk=(n%4)?1:-1;//打表可得
    ll res=0;
    for(int i=1;i<=n;i+=2)
    {
        ll temp=c(n/2-1,i/2);//本质是杨辉三角
        res=(res+(a[i]+mk*a[i+1])*temp+mod)%mod;
    }
    cout<<(res+mod)%mod<<endl;
}

python

import sys
sys.setrecursionlimit(10**5)
MOD = 10**9 + 7
N = 10**5 + 10
a = [0] * N
f = [0] * N
g = [0] * N

def qmi(a, b):
    res = 1
    while b:
        if b & 1:
            res = res * a % MOD
        b >>= 1
        a = a * a % MOD
    return res

def init():  # 预处理
    g[0] = f[0] = 1
    for i in range(1, N):
        f[i] = f[i - 1] * i % MOD
        g[i] = g[i - 1] * qmi(i, MOD - 2) % MOD

def c(n, m):
    if n < m:
        return 0
    return f[n] * g[n - m] % MOD * g[m] % MOD

def main():
    init()
    n = int(input())
    input_list = list(map(int, input().split()))  # 将一行输入按空格分割并转为整数列表
    for i in range(1, n + 1):
        a[i] = input_list[i - 1]  # 把输入列表的值赋给 a 数组

    if n <= 2:  # 特判n<=2的情况
        print((a[1] + a[2]) % MOD)
        return

    if n & 1:  # n为奇数时可以转化成偶数来做
        mk = 1
        for i in range(1, n):
            a[i] = a[i] + a[i + 1] * mk
            mk = -mk
        n -= 1

    mk = 1 if (n % 4) else -1  # 打表可得
    res = 0
    for i in range(1, n + 1, 2):
        temp = c(n // 2 - 1, i // 2)  # 本质是杨辉三角
        res = (res + (a[i] + mk * a[i + 1]) * temp + MOD) % MOD

    print((res + MOD) % MOD)

if __name__ == "__main__":
    main()

java

import java.util.*;
public class Main {
    static final int N = 100010, mod = 1000000007;
    static long[] a = new long[N], f = new long[N], g = new long[N];
    static int n;

    static long qmi(long a, long b) {
        long res = 1;
        while (b != 0) {
            if ((b & 1) != 0) res = res * a % mod;
            b >>= 1;
            a = a * a % mod;
        }
        return res;
    }

    static void init() { // 预处理
        g[0] = f[0] = 1;
        for (int i = 1; i < N; i++) {
            f[i] = f[i - 1] * i % mod;
            g[i] = g[i - 1] * qmi(i, mod - 2) % mod;
        }
    }

    static long c(long n, long m) {
        if (n < m) return 0;
        return f[(int) n] * g[(int) (n - m)] % mod * g[(int) m] % mod;
    }

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        init();
        n = sc.nextInt();
        for (int i = 1; i <= n; i++) a[i] = sc.nextLong();
        if (n <= 2) { // 特判n<=2的情况
            System.out.println((a[1] + a[2]) % mod);
            return;
        }
        if ((n & 1) != 0) { // n为奇数时可以转化成偶数来做
            int mk = 1;
            for (int i = 1; i < n; i++) {
                a[i] = a[i] + a[i + 1] * mk;
                mk = -mk;
            }
            n--;
        }
        int mk = (n % 4 != 0) ? 1 : -1; // 打表可得
        long res = 0;
        for (int i = 1; i <= n; i += 2) {
            long temp = c(n / 2 - 1, i / 2); // 本质是杨辉三角
            res = (res + (a[i] + mk * a[i + 1]) * temp + mod) % mod;
        }
        System.out.println((res + mod) % mod);
    }
}

题目内容

由$n$个整数构成的数组{$a_1,a_2,...,a_n$}，我们有如下操作:

• 你必须在这些整数之间交替写下加减符号，例如假设数组初始值 {$1,2,3,4$}，交替写下加减符号变为$1+2-3+4$;

• 此时会生成第二行数组{$1+2,2-3,3+4$}，即{$3,-1,7$};随后，再次交替写下加减符号变为$3-(-1)+7$(由于上一行末尾是$+$，所以这一行的开头是$-$);

• 此时会生成第三行数组{$4,6$}，继续重复上述操作;

• 直到最后只剩下唯一一个数字时，中止操作，在上方的样例中，最后剩下的数字为$-2$。

  现在，你需要独立求出给定的数组剩下的最后一个值是多少。

输入描述

第一行输入一个整数$n$($1≤n≤10^5$)代表数组中的元素数量。

第二行输入$n$个整数$a_1,a_2,...,a_n$ ($1≤a_i≤10^9$)代表数组元素。

输出描述

在一行上输出一个整数，表示剩下的最后一个值。由于答案可能很大，只需要输出答案对$10^9+7$取模的结果。

样例1

输入

4
1 2 3 4

输出

1000000005

说明

该样例已在题面中说明，注意，负数也需要取模。