思路：动态规划

将所有盒子按照长、宽、高的三个优先级进行从小到大的排序，那么后面的盒子一定不可能放在前面盒子的上面。所以我们排序之后，选择的顺序就已经是定死的从左往右选择了。那么可以使用动态规划进行求解。

定义$dp[i]$表示放上第$i$个盒子所能达到的最大高度，则有

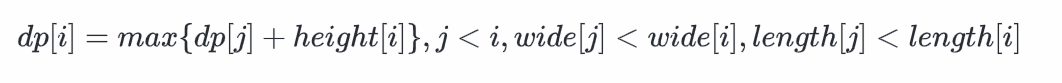
答案为$max{dp[i]},1\le i\le n$

本题为2024年9月11日-华为国内机考原题

华为机考的介绍点击这里

题目内容

圣诞节到了，小塔的妈妈准备了很多圣诞礼盒，礼盒大小不同，小塔在玩堆盒子的游戏，妈妈问小塔，怎么堆盒子使得堆出的高度最高，每个礼盒的大小由长、宽、高表示，堆盒子的时候要求下面的盒子长、宽、高都必须大于上面的盒子，不包含等于。请你帮助小塔一起堆出最高的一堆礼盒，高度为堆出的礼盒的所有高度的总和。

输入描述

输入的第一行是礼盒的个数$N$，

接下来输入$N$行，每行表示每个礼盒的长、宽、高。

礼盒的数量不超过$1000$个，每个盒子的长、宽、高取值范围为$1$~$10$。

输出描述

输出一行，输出能堆出盒子的最高高度

样例1

输入

4
1 1 1
2 3 4
3 6 7
4 5 6

输出

12

说明

选择$1、2、3$，$3$个盒子堆出的高度最高，$1+4+7=12$

样例2

输入

4
1 1 1
1 1 1
2 2 2
2 2 2

输出

3

说明

其中的一种选择方式为选择$1$和$3$两个盒子，堆出的高度最高为$1+2=3$