关键观察

修改最多 K 个位置，等价于保留至少 n-K 个位置不变，并把被修改的位置随意设置，使整个序列满足相邻差不超过 x。 选择一组下标递增的保留位置 $i_1<i_2<\cdots<i_m$；且这些位置的原高度都保留，那么想让中间被修改的位置“补”出来使整段满足条件，必要且充分的是：对所有 p<q，有

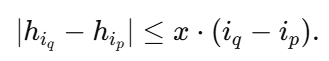
这条条件保证了可以用步长不超过 x 的“线性插值”把中间位置填上。 于是，固定某个 x，问题化为：求一个最长的下标序列，使得任意两点满足上式；记其长度为 L(x)。最少修改数就是 n-L(x)，可行性的判定为

题目内容

小红正在玩一个游戏：这个游戏他需要从左往右依次经过 $n$ 座山，其中第 $i$ 座山的高度为 $h_i$ 。在游戏开始之前，他需要装备耐久足够高的登山鞋才行。

假设小红装备的登山鞋的耐久度为 $x$ ，那么如果存在一个 $i(1≤i<n),|h_{i+1}-h_i|>x$ ，那么小红就无法攀爬下一座山。也就是说，任意相邻的两座山的高度之差不能超过 $x$ 。

游戏正式开始之前，他利用前面关卡获得经验值来购买了 $k$ 次操作，其中每一次操作都可以修改任意一座山的高度，并且可以将其修改为任意非负整数高度。他想知道：自己能够装备的登山鞋的耐久度最低可以是多少?

输入描述

第一行一个正整数 $T$ ，表示数据组数。

对于每一组数据

第一行输入两个正整数 $n$ 和 $k$ ，分别表示山的数量和小红购买的操作次数。

第二行输入 $n$ 个整数 $h_1,h_2,...,h_n$ ，表示山的高度。

$1≤k≤n≤500,1≤T≤50,0≤h_i≤2×10^9$

输出描述

对于每一组数据，输出一行一个整数，表示小红经过若干次操作之后可以装备的登山鞋的最低耐久度。

样例1

输入

3
1 1
2
5 1
1 2 4 7 8
5 3
6 4 7 10 5

输出

0
2
1

说明

第二组样例，可以将序列改为 $1$ $2$ $4$ $6$ $8$ ，这样耐久度就需要 $2$ 。

第三组样例，可以将序列改为 $6$ $6$ $7$ $8$ $9$ ，这样耐久度就需要 $1$ 。