思路

• 状态：设 $dp[i][j]$ 为进入房间 $(i,j)$ 时已获得的最大价值。

• 转移（在网格内 $1 \le i,j \le n$）：

  

  

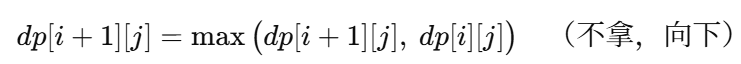
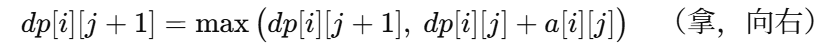
• 初值：$dp[1][1] = 0$（进入起点未拿任何宝藏）。

题目内容

有一座巨大的官殿，可以被视为由$n$行$n$列房间组成，从上到下分别为第$1,2,...n$行,从左到右分别为第$1,2,...n$列。第$i$行第$j$列房间内有价值为$a_{i,j}$的宝藏。

每个房间都有一扇通往下一行同一列的常开的门，即从第$i$行第$j$列房间能移动到第$i+1$行第$j$列房间，但是 如果选择带走房间内的宝藏，则该侧门会关闭。特别地，第$n$行的所有房间的通往下一行同一列的门都通往 宫殿外。

除此之外，每个房间都有通往同一行下一列的门，即第$i$行第$j$列房间有一扇通往第$i$行第$j+1$列房间的门, 该门不常开，但是如果选择带走房间内的宝藏，则该侧门会打开。特别地，第$n$列的所有房间的通往同一行 下一列房间的门都通往宫殿外。

小钟从第一行第一列房间出发，他想知道在离开宫殿前他最多能够带走多少价值的宝藏。请你帮忙计算答案。

输入描述

输入包括多组测试数据。

输入第一行包括一个正整数$T(1<=T<=10)$,表示测试数据的组数。

每组测试数据的第一行有一个整数$n(1<=n<=500)$,表示宫殿由$n$行$n$列房间组成;

接下来的$n$行第$i$行有$n$个整数$a_{i,1},a_{i,2},...,a_{i,n}(0<=a_{i,j}<=10^5)$,依次表示第$i$行第$1,2,....n$列房间内宝藏的价值大小。

保证每个测试点的所有测试数据的$n^2$的和不超过$2.5*10^5$

输出描述

对于每组测试数据,输出一个正整数表示小钟离开宫殿前最多能够带走多少价值的宝藏。

样例1

输入

2
3
1 2 3
4 5 6
7 8 9
2 
0 5
3 1

输出

24
5

说明

对于第一组测试数据，小钟的移动轨迹可以是这样的:$(1,1)\rightarrow(2,1)$$\rightarrow(3,1)\rightarrow(3,2)$$\rightarrow(3,3)\rightarrow$官殿外，分别在$(3,1)，(3,2)，(3,3)$处带走宝藏，总价值大小为$7+8+9=24$

对于第二组测试数据，小钟的移动轨迹可以是这样的:$(1,1)\rightarrow(1,2)\rightarrow$宫殿外，分别在$(1,1),(1,2)$处带走宝藏，总价值大小为$0+5 =5$