- 京ICP备2025123107号-1
- Worker 1, 202ms
- Powered by Hydro v4.18.0 Community
设 f(i) 为用若干个数（每次可取 1..i 中不超过剩余的整数）按顺序恰好凑成和为 i 的方案数。最后一步取值为 t∈[1,i] 时，前缀必须凑成 i−t。因此有纯二重循环的 DP 递推：
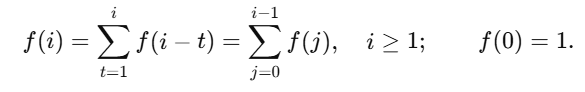
实现上：
dp[0..n]，初始化 dp[0]=1；i=1..n，用第二重循环累加 dp[i]+=dp[i-t] (t=1..i)；dp[n]。优化：定义前缀和
pre[i]=dp[0]+...+dp[i]，可得dp[i]=pre[i-1]、pre[i]=pre[i-1]+dp[i]，从而把计算从 O(n2) 降到 O(n)。
# O(n^2) 动态规划：dp[i] = sum_{t=1..i} dp[i - t]，dp[0]=1
import sys
def count_ways(n: int) -> int:
dp = [0] * (n + 1)
dp[0] = 1 # 空和
for i in range(1, n + 1):
s = 0
# 朴素二重循环：把所有最后一步的取值都枚举一遍
for t in range(1, i + 1):
s += dp[i - t]
dp[i] = s
return dp[n]
def main():
data = sys.stdin.read().strip().split()
n = int(data[0]) # 默认输入合法
print(count_ways(n))
if __name__ == "__main__":
main()
// O(n^2) 动态规划：dp[i] = ∑_{t=1..i} dp[i-t]；dp[0]=1
import java.util.*;
public class Main {
// 外部函数：返回方案数（long）
static long countWays(int n) {
long[] dp = new long[n + 1];
dp[0] = 1L; // 空和
for (int i = 1; i <= n; i++) {
long s = 0L;
for (int t = 1; t <= i; t++) {
s += dp[i - t]; // 枚举最后一步取 t
}
dp[i] = s;
}
return dp[n];
}
// 主函数：ACM 风格输入输出
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt(); // 默认输入合法
System.out.println(countWays(n));
in.close();
}
}
// O(n^2) 动态规划：dp[i] = sum_{t=1..i} dp[i - t]；dp[0]=1
#include <iostream>
#include <vector>
using namespace std;
// 外部函数：返回方案数（long long）
long long countWays(int n) {
vector<long long> dp(n + 1, 0LL);
dp[0] = 1LL; // 空和
for (int i = 1; i <= n; ++i) {
long long s = 0LL;
for (int t = 1; t <= i; ++t) {
s += dp[i - t]; // 枚举最后一步取 t
}
dp[i] = s;
}
return dp[n];
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int n;
if (!(cin >> n)) return 0; // ACM 风格输入
cout << countWays(n) << "\n";
return 0;
}
本题在“每次取 1 或 2 凑成 n”与“每次取 1、2 或 3 凑成 n”的基础上进一步扩展： 给定一个非负整数 n。每次可取一个正整数，取值范围为 1 到 n，将若干个数相加恰好得到 n。两种方案只要在某个位置取的数不同，就视为不同（即顺序有区分）。求不同方案数。
记答案为 f(n)。
4
8