【动态规划5】最长上升子序列

解题思路

本题要求在一个整数序列中找到一个最长的上升子序列，并输出其长度。一个子序列是由原序列中若干个元素（可以不连续）组成的，而上升子序列则要求每一个元素都大于它前面的元素。我们可以使用动态规划的方法高效解决这个问题。通过逐步分析，建立状态转移方程，最终找到最长上升子序列的长度。

Step1: 讨论 $n=3$ 的情况

假设序列长度 $n=3$，且序列为 $a = [3, 1, 2]$。我们需要找到该序列中的最长上升子序列(所有子序列中最长的)。

所有可能的子序列及其长度如下：

1. $[3]$ ：长度为 $1$
2. $[3, 1]$ ：长度为 $2$（不是上升子序列）
3. $[3, 2]$ ：长度为 $2$（不是上升子序列）
4. $[1]$ ：长度为 $1$
5. $[1, 2]$ ：长度为 $2$（上升子序列）
6. $[2]$ ：长度为 $1$

从中可以看出，最长的上升子序列为 $[1, 2]$，其长度为 $2$。将这些方案的集合定义为 $D_3$，即 $D_3 = \{1, 2\}$，其中最大长度为 $2$。

Step2: 情况分类

为了找到序列中的最长上升子序列，首先我们在循环枚举数组a中的每一个元素的适合可以将问题分为以下情况：

1. 当前元素 $a_i$ 单独作为一个新的子序列的一部分：

   即，当前的最长上升子序列仅包含 $a_i$ 本身。

2. 当前元素 $a_i$ 作为前一个子序列的一部分：

   即，将 $a_i$ 加入到之前的某个最长上升子序列中，形成一个更长的上升子序列。

通过这两种情况，我们可以决定是否将当前元素加入到之前的子序列中，或者重新开始一个新的子序列。

Step 3：等价映射

在求解最长上升子序列（LIS）时，我们希望通过动态规划来优化计算。我们将问题拆解为两种情况：

1. 当前元素 $a_i$ 单独作为一个新的子序列的一部分：
   即，我们可以将当前元素 a_i 看作是一个新的上升子序列的起点。在这种情况下，当前子序列的长度就是1，即 dp[i] = 1。

2. 当前元素 $a_i$ 作为前一个子序列的一部分：
   即，当前元素 a_i 可以接在某个之前的上升子序列末尾形成一个新的上升子序列。如果 a_i > a_j（其中 $j < i$），则可以将 a_i 加入到以 a_j 为结尾的上升子序列中。此时，当前子序列的长度将为 dp[j] + 1，即：

通过这两种情况，我们可以决定是否将当前元素加入到之前的子序列中，或者重新开始一个新的子序列。

Step 4：递推方程

对于step1的样例，dp[1]=[3]，对于第二个元素1，

dp[2]=max({[3]+1(不符合因为1<3),[空集]+1})

显然dp[2]=[1]

对于第三个元素2，

dp[3]=max({[3]+2(不符合因为2<3),[1]+2,[空集]+2})

dp[3]=[1,2]

根据等价映射，递推方程和例子可以描述为：

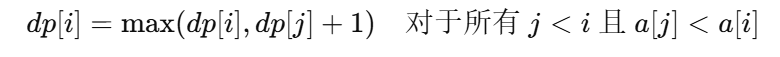
• 解释：
  • dp[i] 表示以 a[i] 为结尾的最长上升子序列的长度。
  • 对于每个 i，我们遍历 j（其中 $j < i$），如果 a[i] > a[j]，那么我们可以更新 dp[i] 为 dp[j] + 1，表示将 a[i] 加入到以 a[j] 为结尾的上升子序列中。

因此，递推方程的含义是：对于每个元素 a[i]，我们通过与所有之前元素进行比较，选择能够形成最长上升子序列的方式。

Step5: 推广情况

对于任意长度为 $n$ 的序列 $a = [a_1, a_2, \dots, a_n]$，定义 $dp[i]$ 表示以第 $i$ 个元素结尾的最长上升子序列的长度。根据递推关系，我们有：

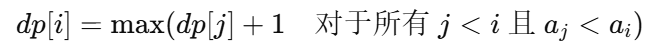
通过迭代计算 $dp[i]$，可以逐步找到整个序列的最长上升子序列的长度。

Step6: 边界条件

在动态规划中，需要明确边界条件来初始化状态转移：

1. 第一个元素的最长上升子序列长度：

   $$dp[1] = 1$$

   因为只有一个元素时，最长上升子序列的长度就是它本身。

2. 对于 $i > 1$ 的元素：

   使用递推方程：

   

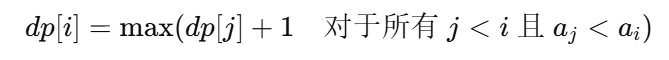
这些边界条件确保了动态规划的递推过程有一个明确的起点。

Step7: 总结

1. 状态定义：

2. 状态转移方程：
   

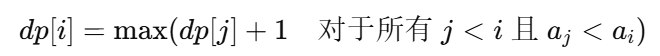
3. 边界条件：

   • $$dp[1] = 1$$

通过动态规划的方法，我们可以高效地计算出序列的最长上升子序列的长度，时间复杂度为 $O(n^2)$，空间复杂度为 $O(n)$。此外，可以通过使用二分查找优化时间复杂度至 $O(n \log n)$，但在本题中 $n \leq 1000$，$O(n^2)$ 已经足够高效。

实现代码

cpp

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

int main() {
    int n;
    cin >> n;  // 输入序列的长度
    vector<int> a(n), dp(n, 1);  // a数组存储序列，dp数组存储以每个元素为结尾的最长上升子序列的长度，初始化为1

    // 读取输入的序列
    for (int i = 0; i < n; i++) {
        cin >> a[i];  // 逐个输入序列中的元素
    }

    // 动态规划部分
    // dp[i] 表示以 a[i] 为结尾的最长上升子序列的长度
    for (int i = 1; i < n; i++) {  // 遍历每一个元素，计算以当前元素为结尾的最长上升子序列
        for (int j = 0; j < i; j++) {  // 遍历当前元素之前的所有元素
            if (a[i] > a[j]) {  // 如果当前元素 a[i] 大于前面元素 a[j]
                dp[i] = max(dp[i], dp[j] + 1);  // 更新 dp[i]，选择增加当前元素的最长子序列长度
            }
        }
    }

    // 输出最长上升子序列的长度
    cout << *max_element(dp.begin(), dp.end()) << endl;  // 输出 dp 数组中的最大值，表示最长上升子序列的长度

    return 0; 
}

python

# 读取数组的长度
n = int(input())  # 输入一个整数 n，表示数组的长度

# 读取数组元素并转换为整数列表
a = list(map(int, input().split()))  # 输入 n 个整数并存储在列表 a 中

# 初始化动态规划数组 dp，长度为 n+1，所有值初始为 1
dp = [1] * (n + 1)  # dp[i] 表示以第 i 个元素结尾的最长递增子序列的长度

# 遍历每个元素，计算最长递增子序列
for i in range(n):
    # 遍历当前元素之前的所有元素
    for j in range(i):
        # 如果当前元素 a[i] 大于之前的元素 a[j]
        if a[i] > a[j]:
            # 更新 dp[i] 为 dp[j] + 1 或当前 dp[i] 的最大值
            dp[i] = max(dp[i], dp[j] + 1)

# 输出 dp 数组中的最大值，即最长递增子序列的长度
print(max(dp))  # 输出结果

java

import java.util.Scanner;

public class LongestIncreasingSubsequence {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        
        // 读取数组的长度
        int n = scanner.nextInt();
        int[] a = new int[n];
        
        // 读取数组元素并存储
        for (int i = 0; i < n; i++) {
            a[i] = scanner.nextInt();
        }
        
        // 初始化动态规划数组 dp，所有值初始为 1
        int[] dp = new int[n];
        for (int i = 0; i < n; i++) {
            dp[i] = 1;
        }
        
        // 遍历每个元素，计算最长递增子序列
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < i; j++) {
                if (a[i] > a[j]) {
                    dp[i] = Math.max(dp[i], dp[j] + 1);
                }
            }
        }
        
        // 找到 dp 数组中的最大值
        int maxLength = 0;
        for (int i = 0; i < n; i++) {
            maxLength = Math.max(maxLength, dp[i]);
        }
        
        // 输出结果
        System.out.println(maxLength);
    }
}

题目描述：

给定一个整数序列，求该序列的最长上升子序列的长度。一个子序列是由原序列中若干个元素（可以不连续）组成的，而上升子序列则要求每一个元素都大于它前面的元素。

输入描述：

• 第一行包含一个整数 $n$，表示序列的长度 $(1 \leq n \leq 1000)$。
• 第二行包含 $n$ 个整数 $a_1, a_2, \dots, a_n$，表示序列中的元素 $(1 \leq a_i \leq 10^9)$。

输出描述：

输出一个整数，表示序列的最长上升子序列的长度。

样例输入：

6
10 9 2 5 3 7

样例输出：

3

提示：

在样例中，最长上升子序列为 [2, 5, 7]，其长度为 3。