判断二叉树是否轴对称

题目理解

题目要求检查一棵二叉树是否是轴对称的，即判断这棵树是否为镜像二叉树。镜像二叉树的定义是：对于树中的每一个节点，其左子树与右子树互为镜像。

解题思路

递归方法

Leetcode 39.对称二叉树-原题链接

题目内容

给你一个二叉树的根节点 $root$ ， 检查它是否轴对称。

输入描述

一行包含二叉树的序列化数组，节点值之间用空格隔开，空节点用null表示。

输出描述

• 若二叉树是轴对称的，输出 true；
• 否则，输出 false。

样例1

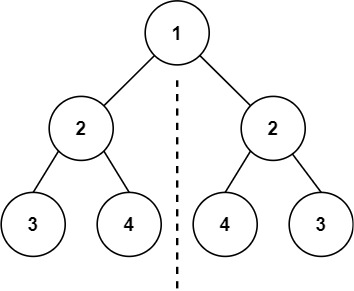
输入

1 2 2 3 4 4 3

输出

true

样例2

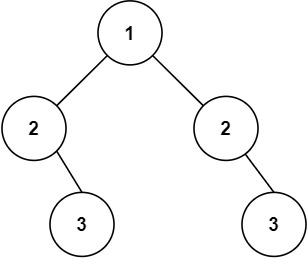
输入

1 2 2 null 3 null 3

输出

false

提示

• 树中节点数目在范围 $[0, 100]$ 内
• $-100 <= Node.val <= 100$